Week 1 Notes
What is a Set? green
- A set is simply a collection of objects.
- Sets can contain an infinite number of items.
- e.g. \(\mathbb{N}\) is the set of all natural numbers.
- Order of elements is ignored, as well as all duplicate elements.
Notation green
- \(x \in A\) means \(x\) is a member of set \(A\)
- \(A \subseteq B\) means set \(A\) is a subset of set \(B\)
- \(A \subset B\) means set \(A\) is a subset of set \(B\) but \(A \neq B\)
- \(A \subsetneq\) means set \(A\) is not a subset of \(B\)
- \(| A |\) means the cardinality of set \(A\) (aka the number of elements in set \(A\))
How to define sets green
Basic definitions
- \(\{1,3,5,7,9\}\)
- \(\{1,\dots,100\}\)
- \(\{1,3,\dots,101\}\)
More complex definitions
- \(\{\underbrace{ x+3 }_{ \text{Pattern for result} } |\text{ }\underbrace{ x \in \{1,\dots,100\} }_{ \text{Generator} },\text{ }\underbrace{ x<10 \text{ and x is odd} }_{ \text{Filter (Condition)} }\}\) turns into \(\{4,6,8,10,12\}\)
Power Sets green
- Its useful to be able to consider all subsets of a set.
- Given any set \(A\) we define the power set of \(A\), denoted \(\mathcal{P} (A)\), to be the set of all subsets of \(A\)
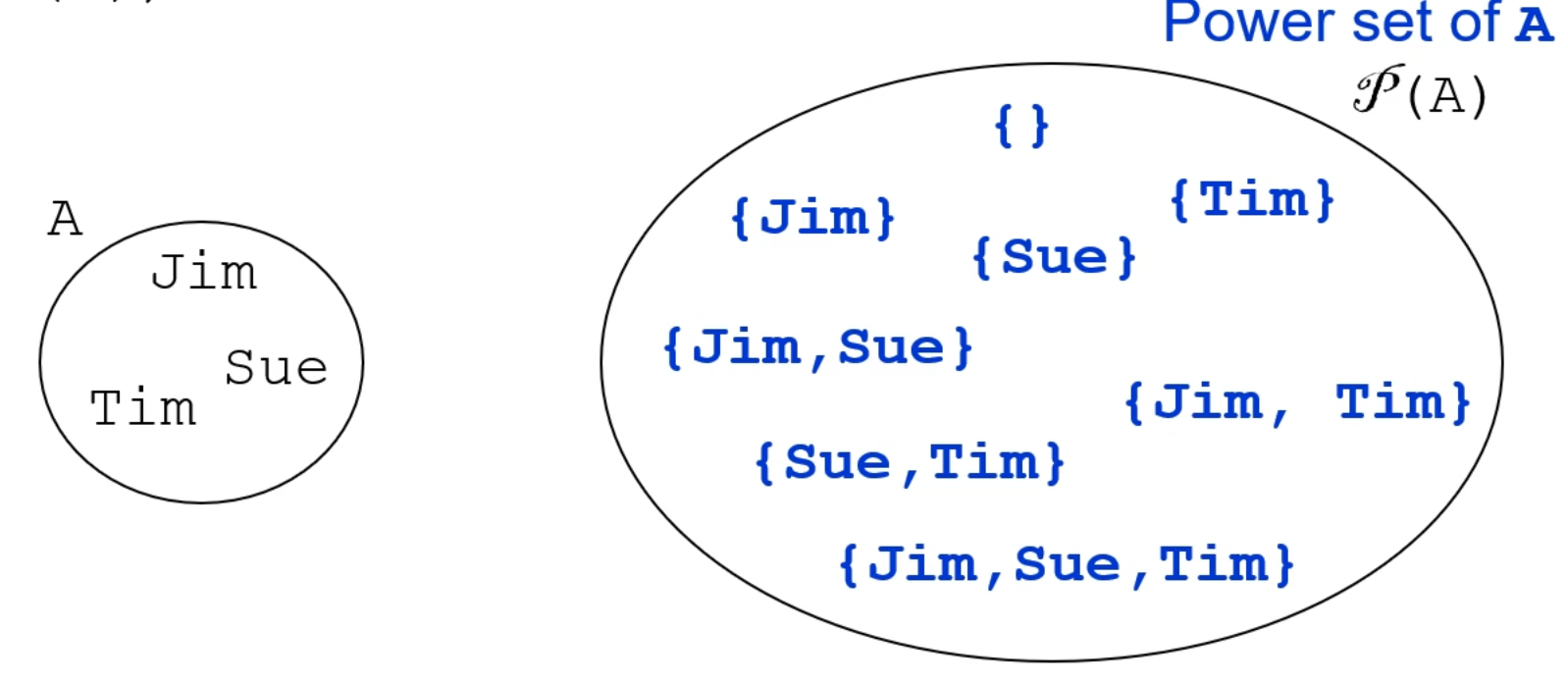 Important
Important
- If a set \(A\) has \(N\) values in it, then \(\mathcal{P} (A)\) will have \(2^{N}\) values in it.
Power Set Examples
- \(\mathcal{P} (\{a\}) = \{\{\},\{a\}\}\)
- If \(A = \{a,b,c,d\}\), then there will be \(2^4\) values in \(\mathcal{P} (A)\) which is \(16\)
Pairs in sets green
- Idea is that when given two sets \(A\) and \(B\), we can have a pair \((x,y)\) where \(x \in A\) and \(y \in B\)
- e.g. \(A=\{\text{tea},\text{coffee}\}\) and \(B=\mathbb{R}\) yields results such as \((\text{tea},1.82)\) and \((\text{coffee},422)\)
- Important to remember that in a pair, order is important, i.e. \((x,y)\) isn't the same as \((y,x)\)
Cartesian Product green
- Let \(A\times B\) denote the set of all pairs over \(A\) and \(B\)
- This is defined by \(A\times B=\{(x,y)|x\in A,y\in B\}\)
- \(A\times B\) is referred to as the Cartesian product of \(A\) and \(B\)
Example: If \(A=\{1,2,3\}\) and \(B={a,b}\) then \(A\times B = \{(1,a),(1,b),(2,a),(2,b),(3,a),(3,b)\}\)