Notes

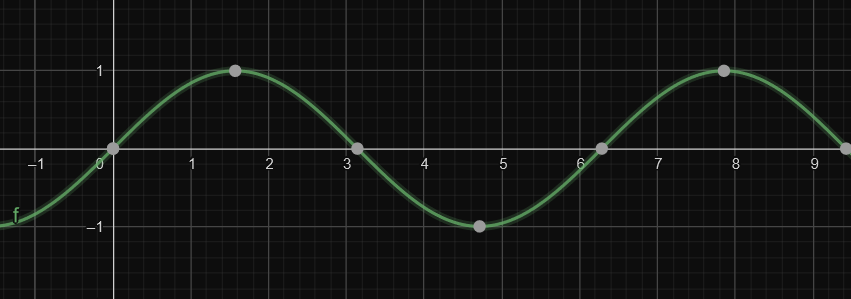
sin(x) and cos(x)

Find the exact values of:

\(\sin\left( \frac{\pi}{6} \right)=\frac{1}{2}\)
\(\cos\left( \frac{\pi}{2} \right)=0\)
\(\sin\left( \frac{\pi}{4} \right)=\frac{1}{\sqrt{ 2 }}\)
\(\tan\left( \frac{\pi}{3} \right)=\sqrt{ 3 }\)
\(\cos\left( \frac{\pi}{3} \right)=\frac{1}{2}\)
\(\sin\left( \frac{2\pi}{3} \right)=\frac{\sqrt{ 3 }}{2}\)
\(\tan\left( \frac{3\pi}{4} \right)=-\tan\left( \frac{\pi}{4} \right)=-1\)
\(\cos\left( \frac{5\pi}{6} \right)=-\cos \left( \frac{\pi}{6} \right)=-\frac{\sqrt{ 3 }}{2}\)
\(\tan\left( \frac{5\pi}{3} \right)=-\tan\left( \frac{\pi}{3} \right)=-\sqrt{ 3 }\)
\(\cos\left( \frac{5\pi}{4} \right)=-\cos\left( \frac{\pi}{4} \right)=-\frac{\sqrt{ 2 }}{2}\)
\(\sin\left( -\frac{\pi}{6} \right)=-\frac{1}{2}\)
\(\tan\left( -\frac{5\pi}{6} \right)=\tan\left( \frac{\pi}{6} \right)=\frac{\sqrt{ 3 }}{3}\)
\(\sin 3\pi=\sin \pi=0\)

Degrees to Radians

\(180^{\circ}=\pi\)
\(30^{\circ}=\frac{\pi}{6}\)
\(45^{\circ}=\frac{\pi}{4}\)
\(720^{\circ}=4\pi\)
\(18^{\circ}=\frac{\pi}{10}\)
\(120^{\circ}=\frac{2\pi}{3}\)
\(15^{\circ}=\frac{\pi}{12}\)
\(40^{\circ}=\frac{4\pi}{18}\)
\(270^{\circ}=\frac{3\pi}{2}\)
\(7.5^{\circ}=\frac{\pi}{24}\)
\(144^{\circ}=\frac{4\pi}{5}\)
\(220^{\circ}=\frac{11\pi}{9}\)

Radians to Degrees

\(2\pi=180^{\circ}\)
\(\frac{\pi}{3}=60^{\circ}\)
\(\frac{\pi}{2}=90^{\circ}\)
\(\frac{3\pi}{4}=135^{\circ}\)
\(\frac{\pi}{18}=10^{\circ}\)
\(\frac{\pi}{30}=6^{\circ}\)
\(\frac{5\pi}{6}=150^{\circ}\)
\(\frac{\pi}{8}=22.5^{\circ}\)
\(3\pi=420^{\circ}\)
\(\frac{2\pi}{15}=25^{\circ}\)
\(\frac{7\pi}{3}=420^{\circ}\)
\(\frac{9\pi}{20}=81^{\circ}\)

Radian Measure