Stationary Points

A stationary point is a point on a curve where the gradient is 0.
You can determine weather a stationary point is a local maximum, a local minimum or a point of inflection by looking at the gradient of the curve of either side.
For any point on the curve \(y=f(x)\) where \(f^{'}(x)=0\) is called a stationary point.

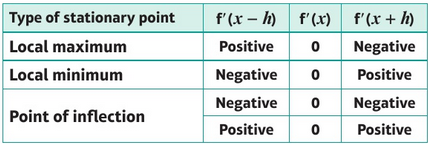
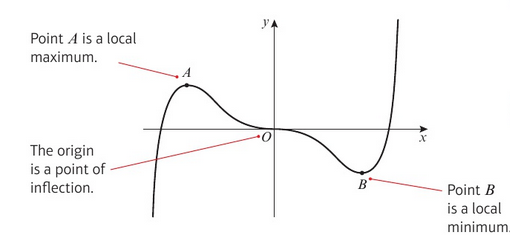
Using the second derivative to find the nature of a stationary point.

If a function \(f(x)\) has a stationary point when \(x=a\):
If the second derivative of \(f(a)>0\) then the point is a local minimum.
If the second derivative of \(f(a)<0\) then the point is a local maximum.
If the second derivative of \(f(a)=0\) then the point could be a local maximum, or a local minimum or a point of inflection. You have to look at the points on either side to see which it is.

Find the coords of the stationary point on the curve \(y=x^4-32x\)

\(\frac{dy}{dx}=4x^3-32\)
Turning point: \(4x^3-32=0\)
\(4x^3=32\)
\(x^3=8\)
\(x=2\)
Sub back in \(x\): \(2^4-32\times 2=-48\)
\(\therefore (2,-48)\) is a stationary point.

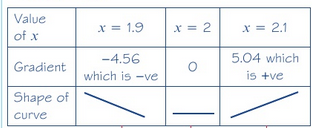
The curve with equation \(y=x^2-32\sqrt{ x }+20, x>0\) has a stationary point \(P\). Use calculus to find the coordinates of \(P\) and to determine the nature of P.

First derivative: \(y=2x-16x^{-\frac{1}{2}}\)
Set = 0: \(2x=\frac{16}{x^{\frac{1}{2}}}\)
\(2x^{\frac{3}{2}}=16\)
\(x^{\frac{3}{2}}=8\)
\(x=4\)

Sub back in for y-coord: \(y=4^2-32\sqrt{ 4 }+20\)
\(=16-64+20\)
\(=-28\)
Coords = \((4, -28)\)

Now find second derivative: \(\frac{d^2y}{dx^2}=2+8x^{-\frac{3}{2}}\)
Sub in: \(=2+8(4)^{-\frac{3}{2}}\)
\(=3\)

\(\frac{d^2y}{dx^{2}}>0 \therefore\) it is a minimum point.

By finding the stationary points, sketch the graph of \(y=\frac{1}{x}+27x^3\)

First derivative: \(y=\frac{1}{x^2}+81x^2\)
Set to 0: \(\frac{1}{x^2}+81x^{2} =0\)
\(81x^2=\frac{1}{x^2}\)
\(81x^4=1\)
\(x=\frac{1}{3}\) or \(-\frac{1}{3}\)
Sub back in for y-coord:\(y=4\) or \(-4\)
Stationary points are: \(\left( \frac{1}{3}, 4 \right)\) and \(\left( -\frac{1}{3}, -4 \right)\)

Stationary Points

Backlinks