The Big-M Method
Big M method
- M is used to represent a massive number labelled M.
- This number M is begger than any number that will ever be written ever.
- This can be used to drive the artificial veriables towards 0.

Big-M Method by example
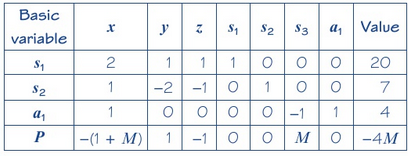
- Maximise \(P=x-y+z\) subject to:
- \(2x+y+z\leq 20\)
- \(x-2y-z\leq 7\)
- \(x\geq 4\)
- \(x, y, z\geq 0\)
. - \(2x+y+z+s_{1}=20\)
- \(x-2y-z+s_{2}=7\)
- \(x-s_{3}+a_{1}=4\)
- \(x,y,z,s_{1},s_{2},s_{3},a_{1}\geq0\)
- \(P=x-y+z-Ma_{1}\)
- \(a_{1}=4-x+s_{3}\)
This gives: - \(P=x-y+z-M(4-x+s_{3})=(1+M)x-y+z-Ms_{3}-4M\)
Which rearranges to: - \(P-(1+M)x+y-z+Ms_{3}=-4M\)
The tabloux is now written as: