Linear Transformations in three dimensions
3D Transformations
- You can use unit vectors in 3d too
- If you have \(i\), \(j\) and \(k\) as your unit vectors and have a reflection in the plane \(z=0\), then our k componant will be negative.

Rotate by angle \(\theta\) about the y-axis
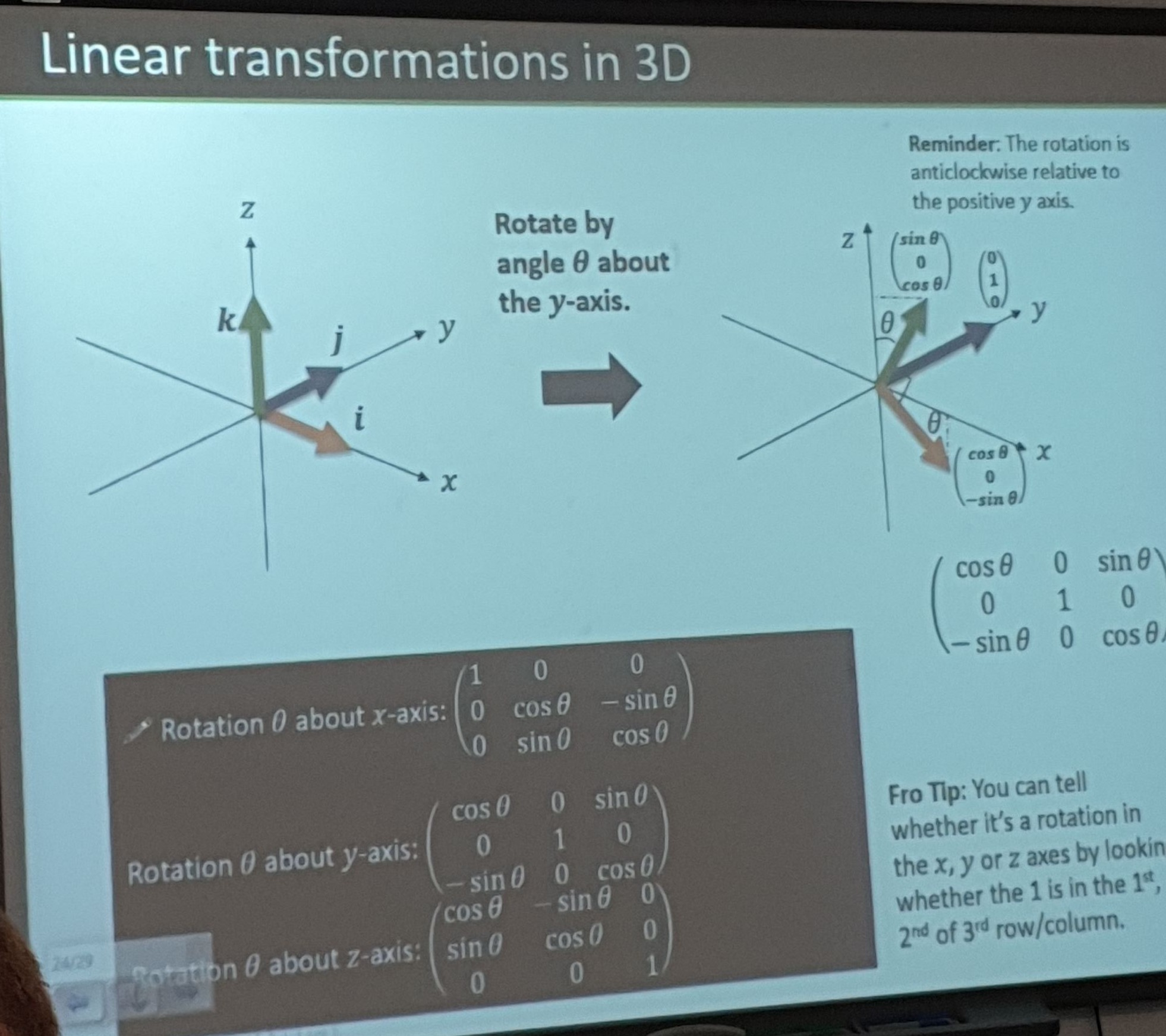
- It helps to imagine that you are standing on the blue line in this image and looking back at the two axis' and turning them like a wheel.
Rotation in 3 dimentions
- \(\begin{pmatrix}\frac{\sqrt{ 3 }}{2} & 0 & \frac{1}{2} \\0 & 1 & 0 \\-\frac{1}{2} & 0 & \frac{\sqrt{ 3 }}{2}\end{pmatrix}\)
- Compare this to the ones we saw in the image above and we get that this is a rotation in the y axis.