Solving Systems of Equations using Matrices

Solving a simple simultaneous equation

\(\begin{pmatrix}2x+2y \\ 3x-5y\end{pmatrix}=\begin{pmatrix}10 \\ -9\end{pmatrix}\)
Rewritten, this gives us:
\(\begin{pmatrix}2 & 2 \\ 3 & -5\end{pmatrix}\begin{pmatrix}x \\ y\end{pmatrix}=\begin{pmatrix}10 \\ -9\end{pmatrix}\)
When we want to solve these, we want \(x\) and \(y\).
To solve this we can rearrange the matrices.
\(\mathbf{A}x=\mathbf{B}\)
\(\mathbf{A^{-1}A}x=\mathbf{A^{-1}B}\)
\(\mathbf{I}x=\mathbf{A^{-1}B}\)
\(x=\mathbf{A^{-1}B}\)

We can now apply these facts to our new matrix.
\(\begin{pmatrix}x \\ y\end{pmatrix}=\frac{1}{16}\begin{pmatrix}5 & 2 \\ 3 & -2\end{pmatrix}\begin{pmatrix}10 \\ -9\end{pmatrix}\)
\(\frac{1}{16}\begin{pmatrix}50-18 \\ 30+18\end{pmatrix}\)
\(\frac{1}{16}\begin{pmatrix}32 \\ 48\end{pmatrix}\)
\(\begin{pmatrix}2 \\ 3\end{pmatrix}\)

The rule

Applying this to a 3 unknown problem

\(-x+6y-2z=21\)
\(6x-2y-z=-16\)
\(-2x+3t+5z=24\)

This can be written as:
\(\begin{pmatrix}-1 & 6 & -2 \\ 6 & -2 & -1 \\ -2 & 3 & 5\end{pmatrix}\begin{pmatrix}x \\ y \\ z\end{pmatrix}=\begin{pmatrix}21 \\ -16 \\ 24\end{pmatrix}\)
The inverse of the 3x3 matrix is: \(\begin{pmatrix}\frac{1}{27} & \frac{4}{21} & \frac{10}{189} \\ \frac{4}{27} & \frac{1}{21} & \frac{13}{189} \\ -\frac{2}{27} & \frac{1}{21} & \frac{34}{189}\end{pmatrix}\)
\(\therefore \begin{pmatrix}x \\ y \\ z\end{pmatrix}=\begin{pmatrix}\frac{1}{27} & \frac{4}{21} & \frac{10}{189} \\ \frac{4}{27} & \frac{1}{21} & \frac{13}{189} \\ -\frac{2}{27} & \frac{1}{21} & \frac{34}{189}\end{pmatrix}\begin{pmatrix}21 \\ -16 \\ 24\end{pmatrix}=\begin{pmatrix}-1 \\ 4 \\ 2\end{pmatrix}\)
Therefore our answers are \(x=-1\), \(y=4\), \(z=2\).

Applying this to a modelling question

What if the simultaneous equations never meet?

If the simultaneous equations never meet then the matrix that defines them does not have an inverse. This means it is singular.
This applies for all types of simultaneous equations, e.g. equations with 3 unknowns gives a point in 3d space. However this can not be visualised well with 4+ dimensions due to the 3d nature of reality.

3 variables, 3 dimensions

In 3d space with 3 unknowns, a simultaneous equation with 3 unknowns will be visualised as a plane. (think like a sheet of paper).
We get a solution when all 3 planes intersect with one another.
The equation for a plane is: \(ax+by+cz=d\) instead of the 2 dimensional \(ax+by=c\) or \(y=mx+c\).
This gives us a straight line
This give a single point in space
This forms a prism which has NO solutions. This means there is not point where all 3 planes intersect.
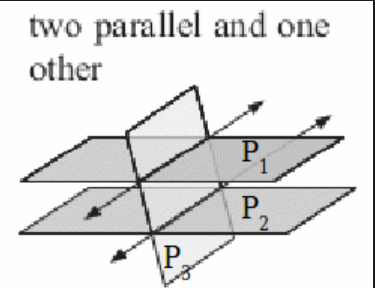
Again, no solutions because there is no intersecting point. In this case it is because 2/3 planes are parallel.

How to write the conclusions

If there is no point where the planes intersect, the system of equations is inconsistant.
If there all intersect at one point and one point only, then the matrix is singular, otherwise it is always non-singular.

Finding the type of system

If 2 equations are the same (e.g. \(x+y+z=1\) and \(2x+2y+2z=2\)) then these two planes are the same plane.
If two equations are the same and have different final numbers (e.g. \(x+y+z=1\) and \(x+y+z=5\)) then these two equations are parallel.
To find if a system makes a prism or a sheath we can subtract one eqaution from another to eliminate a variable.
e.g. \(3x+6y-6z=-6\), \(-6x+3y+3z=2\) and \(-3x-y+3z=-2\)
EQ1+2(EQ2) = \(-9x+12y=-2\)
EQ2-EQ3=\(-3x+4y=4\)
From this we can see that the equations are not multiples of one another, therefore they form a prism.
If you eliminate \(z\) from all 3 equations using EQ1-EQ2, EQ2-EQ3 and EQ3-EQ1, and all 3 equations are multiples of one another then the equations form a sheath.

Backlinks