Linear Programming Methods
Intro to Linear Programming
- Label the region R where \(2x+y<=10\), \(y<-1\) and \(y<x\)
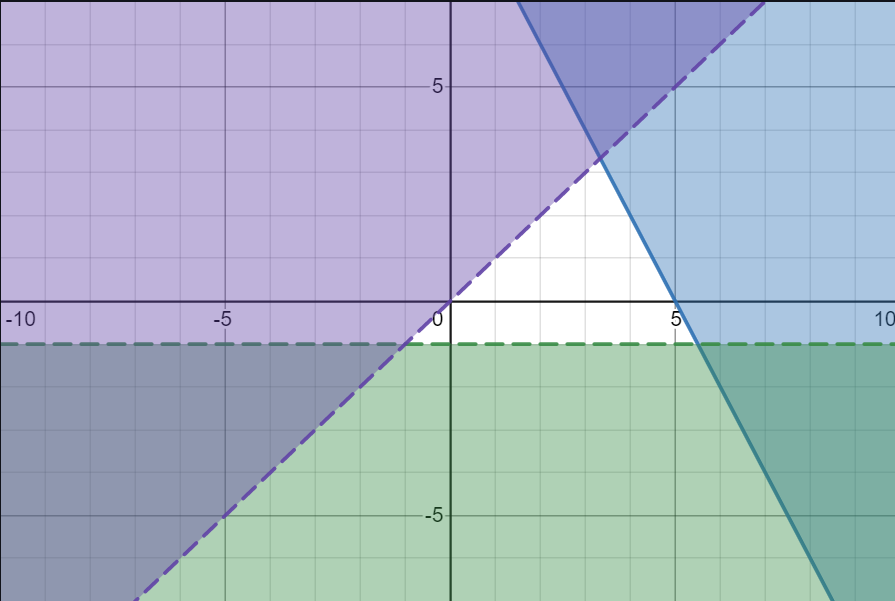
Mental exercise
- Label the region R where \(x>1000\), \(y>500\), \(x+2y<4000\) and \(x<y\).
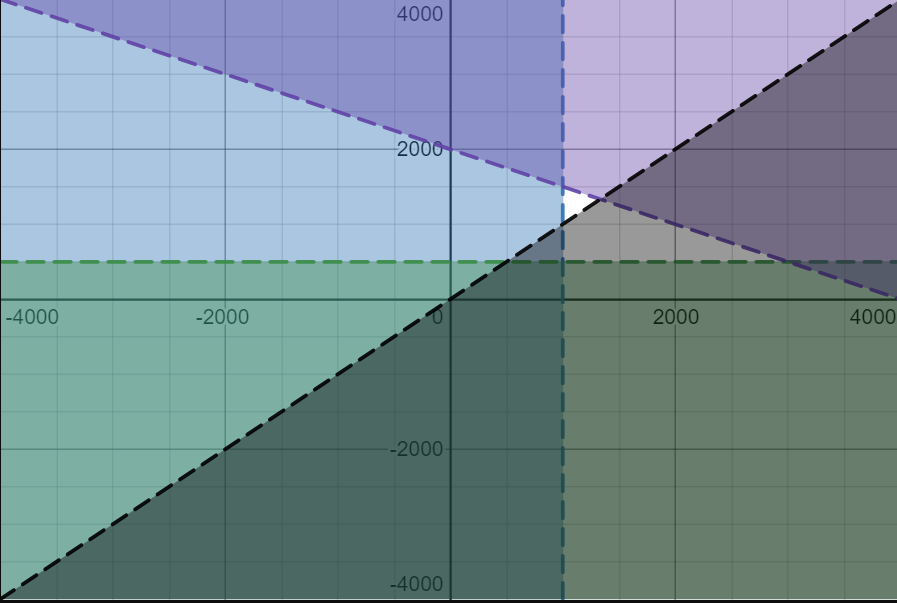
In this example, x = toy aarkvarks and y = toy donkeys produced by a toy company. In real life, a company might have a contract to produce a certain amount of products.
The inequalities used to descibe the graph are called constraints.
For this graph, any point inside the white area is valid and any point outside the white area is invalid
Now the problem, find the co-ordinates of the triangle of region R. - \(A: (1000, 1500)\)
- \(B: \left( \frac{4000}{3}, \frac{4000}{3} \right)\)
- \(C: (1000, 1000)\)
For the most profit/items sold, B is the best due to x+y being the biggest out of the three points.
If Y, (donkeys) is priced higher, then A could be a better strategy.
Another mental exercise
- A company manafactures computer screens and phone screens.
- Maximum daily output is 8000 screens.
- It must make at least 1000 phone screens.
- There must be at least twice as many phone screens as computer screens.
- Write these constraints in algebraic form.
\(x\) is phone screens
\(y\) is computer screens
- \(x+y\leq8000\)
- \(x\geq1000\)
- \(x\geq 2y\)

\(A=(1000,0)\)
\(B=(1000, 500)\)
\(C=\left( \frac{16000}{3} , \frac{8000}{3}\right)\) (Simultaneous equations to solve)
\(D=(8000, 0)\)
Greatest Profit (P=x+10y):
\(A=1000\)
\(B=6000\)
\(C=32,000\)
\(D=8000\)
In this type of problem, the answers HAVE to be integer values. This is because in a real life scenario you cannot have a fraction amount for products produced.