Forces on Charged Particles
Charged Particles in a magnetic field
- A force acts on a charged particle moving in a magnetic field.
- This is why a current-carrying wire experiences a force in a magnetic field — electric current in a wire is the flow of negatively charged electrons.
- The force on a current-carrying wire in a magnetic field perpendicular to the current is given by F = BIL
- Electric current, I, is the flow of charge, Q, per unit time, t. So \(I=\frac{Q}{t}\)
- A charged particle which moves a distance I in time t has a velocity, \(v = \frac{l}{t}\), so \(l=vt\)
- Putting all these equations together gives the force acting on a single charged particle moving through a magnetic field, where its velocity is perpendicular to the magnetic field:
\[F=BQv$$
- Where:
- $F$ = force
- $B$ = Magnetic Field Strength
- $Q$ = Charge
- $v$ = Velocity (in $m/s$)
---
- As a particle movies through a magnetic field, it is unlikely to be moving perpendicular to the field lines. If it's velocity vector is at an angle $\theta$ to the field lines, then the formula becomes:
$$F=BQv\sin(\theta)\]
Motor force acting on particles
- The motor force acts on individual particles in exactly the same way as it does on a current carrying wire, this is because it is the eletrons in the wire that feel the force.
- This effect is used in particle accelerators to both steer the particles around the circular path and also to analyse the new particles created as find out their properties.
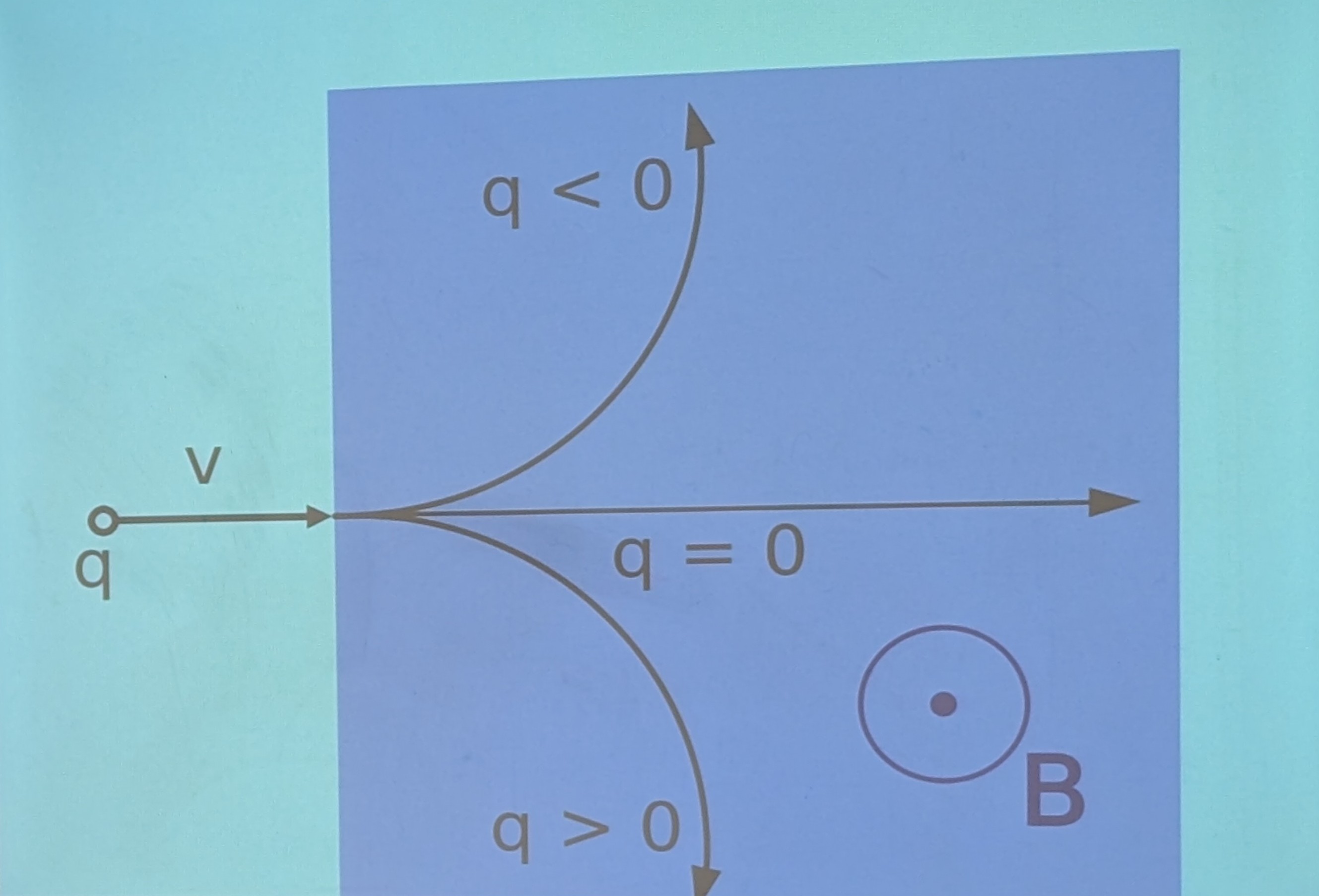
The circular path of particles
Three simple rules
- The motor force is always perpendicular to the velocity vector of the particle so no work is done.
- Flemming's left hand rule shows that the motor force is continually perpendicular to the motion of the particle so the particle will trace out a circular path.
- The force causes an acceleration but not a change in speed so it is a centripetal force.
Equation
\[r=\frac{mv}{BQ}\]