The Chain Rule
Chain Rule
\[\frac{dy}{dx}=\frac{dy}{du}\times \frac{du}{dx}\]
How to use the Chain Rule
- The Chain Rule can be used to differentiate composite functions. This means a function inside of another function.
- e.g. \(\ln(\sin(x))\) has the outer function \(\ln()\) and the inner function \(\sin()\)
- The chain rule states that:
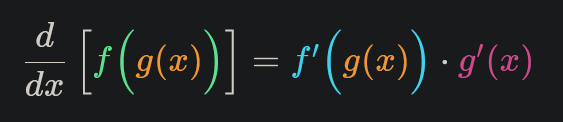
\((3x-1)^{15}\)
- \((3x-1)^{15}\)
- \(15(3x-1)^{14}\times 3\)
- \(45(3x-1)^{14}\)
\((4x^2-7)^{10}\)
- \((4x^2-7)^{10}\)
- \(10(4x^2-7)^9\times 8x\)
- \(80x(4x^2-7)^9\)
\(e^{x^2+x}\)
\(e^{x^2+x}\)
\((2x+1) e^{x^2+x}\)
\(\frac{3}{(x^2-1)^4}\)
- \(\frac{3}{(x^2-1)^4}\)
- \(3(x^2-1)^{-4}\)
- \(-4\times3(x^2-1)^{-5}\times 2x\)
- \(-24x(x^2-1)^{-5}\)
- \(\frac{-24x}{(x^2-1)^5}\)