Harder Trigonometric Equations
REMEMBER
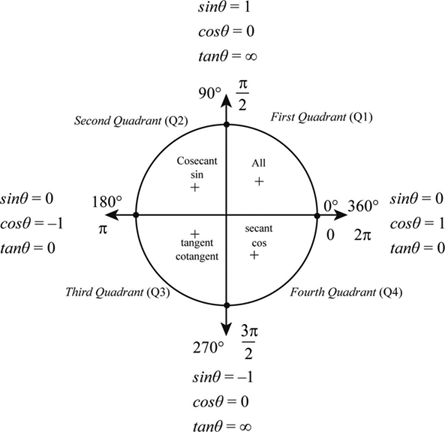 and
and

Sub in A:
- \(A = 2x+30\)
- \(\sin A = \frac{1}{\sqrt{ 2 }} 30 \leq A\leq 750\)
- \(A = \sin^{-1}\left( \frac{1}{\sqrt{ 2 }} \right) = 45^\circ\)
Draw cast diagram:
- \(A_{1} = 45\)
- \(A_{2} = 135\)
- \(A_{3} = 405\)
- \(A_{4} = 495\)
- \(X_{1} = 7.5\)
- \(X_{2} = 52.5\)
- \(X_{3} = 187.5\)
- \(X_{4} = 232.5\)
Divide both sides by cos(x):
- \(\tan x = 2\)
- \((x = tan^{-1} 2) = 63.43^\circ\)
Sub in A:
\(A = 3x-10^\circ\)
\(\cos A = -0.4\)
\(\cos-0.4 = 113.58^\circ\) in the interval \(-10 \leq x \leq 530\)
Going all the way round the cast diagram:
\(180^\circ - 113.58^\circ = 66.42^\circ\)
On a cast diagram:
\(A_{1} = 113.58\)
\(A_{2} = 246.42\)
\(A_{3} = 473.58\)
\(X_{1} = 41.19\)
\(X_{2} = 85.47\)
\(X_{3} = 161.19\)
Let \(x = \sin x\):
- \(5x^2+3x-2=0\)
Factorise:
- (5x-2)(x+1) = 0
- \(x=\frac{2}{5}\) and \(x=-1\)
Sub in:
- \(\sin x=\frac{2}{5}\) and \(\sin x=-1\)
- \(x = \sin^{-1}\left( \frac{2}{5} \right)\)
\(x_{1} = 23.58^\circ\)
\(x_{2} = 180-23.58 = 156.42^\circ\)
\(x_{3} = 270^\circ\)
\(\tan\theta = 2\)
\(\tan^{-1}2 = 63.43^\circ\)
\(x_{1} = 63.43\)
\(x_{2} = 116.57^\circ\)
\(x_{3} = -63.43^\circ\)
\(x_{4} = 296.57^\circ\)
Do later