Determinants
2x2 matrices
Matricies as a function
- Matrices can be thought of as a function to transform a point.
- \(\begin{pmatrix}1 & 2 \\ 3 & 4\end{pmatrix}\begin{pmatrix}1 \\ 1\end{pmatrix}=\begin{pmatrix}3 \\ 7\end{pmatrix}\)
- Now the question is, is there an inverse function that can transform the point (3, 7) back into it's original (1, 1)?
- This matrix would be called the inverse matrix.
Determinants
- The determinant of a matrix \(\mathbf{A}=\begin{pmatrix}a & b \\ c & d\end{pmatrix}\) is det\((\mathbf{A})=|\mathbf{A}|=ad-bc\)
- If det\((\mathbf{A})=0\), then \(\mathbf{A}\) is a singular matrix and it does not have an inverse.
- If det\((\mathbf{A})\) \(\cancel{ = }0\), then \(\mathbf{A}\) is a non-singular matrix and does have an inverse.
Determinant Questions 2x2
- Given that \(\mathbf{A}\) is singular, find the value of \(p\).
\(\mathbf{A}=\begin{pmatrix}4 & p+2 \\ -1 & 3-p\end{pmatrix}\)
\((12-4p)-(-p-2)=12-4p+p+2=0\)
\(14-3p=0\)
\(14=3p\)
\(p=\frac{14}{3}\)
- \(\mathbf{A}=\begin{pmatrix}a & -5 \\ 2 & a+4\end{pmatrix}\) where \(a\) is real.
\(\det(\mathbf{A})=a^2+4a+10\)
\(b^2-4ac\)
\(4^2-40<0\)
Therefore \(A\) is non-singular.
3x3 matrices
3x3 Matrices
\(\(\begin{pmatrix}a & b & c \\d & e & f \\g & h & i\end{pmatrix}=a\begin{pmatrix}e & f \\h & i\end{pmatrix}-b\begin{pmatrix}d & f \\g & i\end{pmatrix}+c\begin{pmatrix}d & e \\g & h\end{pmatrix}\)\)
1. 
2. 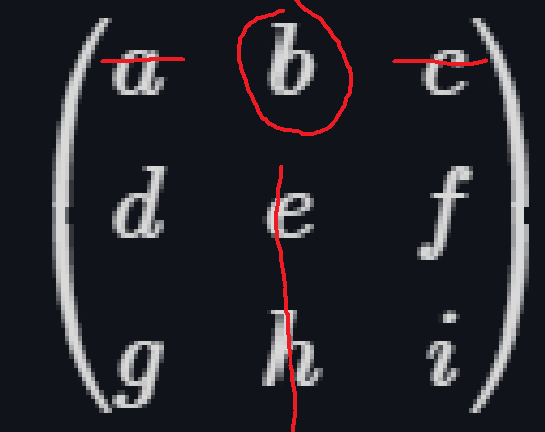
3. 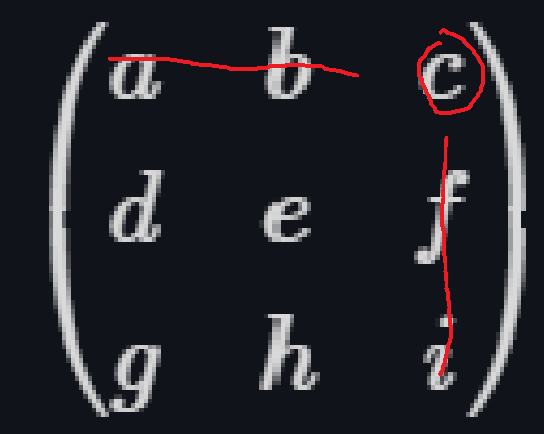
\(\mathbf{A}=\begin{pmatrix}3 & k & 0 \\ -2 & 1 & 2 \\ 5 & 0 & k+3\end{pmatrix}\). Given that A is singular, find all values of \(k\)
- \(3\begin{pmatrix}1 & 2 \\ 0 & k+3\end{pmatrix}-k\begin{pmatrix}-2 & 2 \\ 5 & k+3\end{pmatrix}+0\text{ (irrelevant)}\)
- \(3(k+3)-k(-2k-16)=3k+9+2k^2+16k=2k^2+19k+9\)
- \((2k+1)(k+9)=0\)
- \(k=-\frac{1}{2}\), \(k=-9\)
Minors
Minors
- To find the minor of an element of a 3x3 matrix, cross out the rows and columns from where your element is, then put the rest of the elements not crossed out into a 2x2 matrix.
- Find the determinant of this 2x2 matrix, and this value is the minor of the element you started with.
Finding Minors
Find the minor of \(k\) in this matrix.
- \(\begin{pmatrix}2 & 9 & -3 \\ 5 & k & 0 \\ 3 & -9 & 7\end{pmatrix}\)
- Form into new matrix: 
- New matrix = \(\begin{pmatrix}2 & -3 \\ 3 & 7\end{pmatrix}\)
- Determinant of this matrix = \(14-(-9)=23\)
- \(23\) is the minor of the element \(k\)