Volumes of Revolution around the x-axis
Volumes of Revolution
- You can use Integration to find volumes of revolution such as cones.
- If we have a diagonal line and rotate it around the x-axis, the 3d shape formed is a cone.
- Instead of summing an infinite amount of rectangles in normal integration, we instead sum an infinite amount of circular strips.
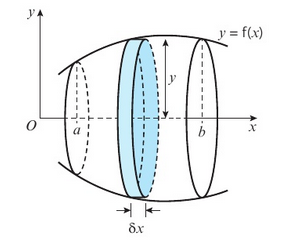
- The equation for a volume of revolution is: $$V=\pi \int ^a_{b}y^2 \, dx $$
Deriving the equation of a sphere
- If we have a circle of equation \(x^2+y^2=R^2\) we can rearrange this to be \(y^2=R^2-x^2\).
- We are now integrating between \(R\) and \(-R\).
- \(V=\pi\int ^R_{-R}y^2 \, dx\)
- \(V=\pi\int ^R_{-R}R^2-x^2 \, dx\)
- \(\pi\left[ R^2x-\frac{1}{3}x^3 \right]^R_{-R}\)
- \(\pi\left[ \left( R^3-\frac{1}{3}R^3 \right)-\left( -R^3+\frac{1}{3}R^3 \right) \right]\)
- \(\pi\left( \frac{6}{3}R^3 -\frac{2}{3}R^3\right)\)
- \(\frac{4}{3}\pi R^3\)
\(y=10x^2\) between \(x=0\) and \(x=2\)
- \(V=\pi \int ^2_{0}10x^2 \, dx\)