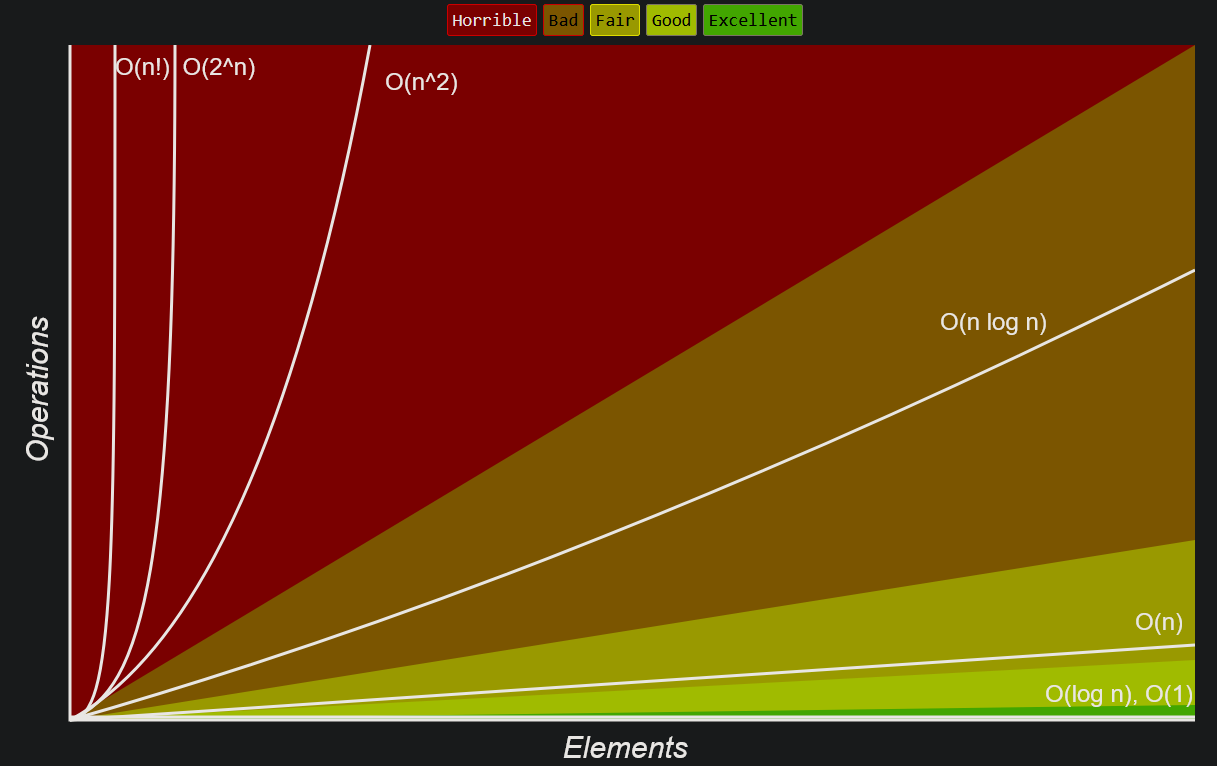
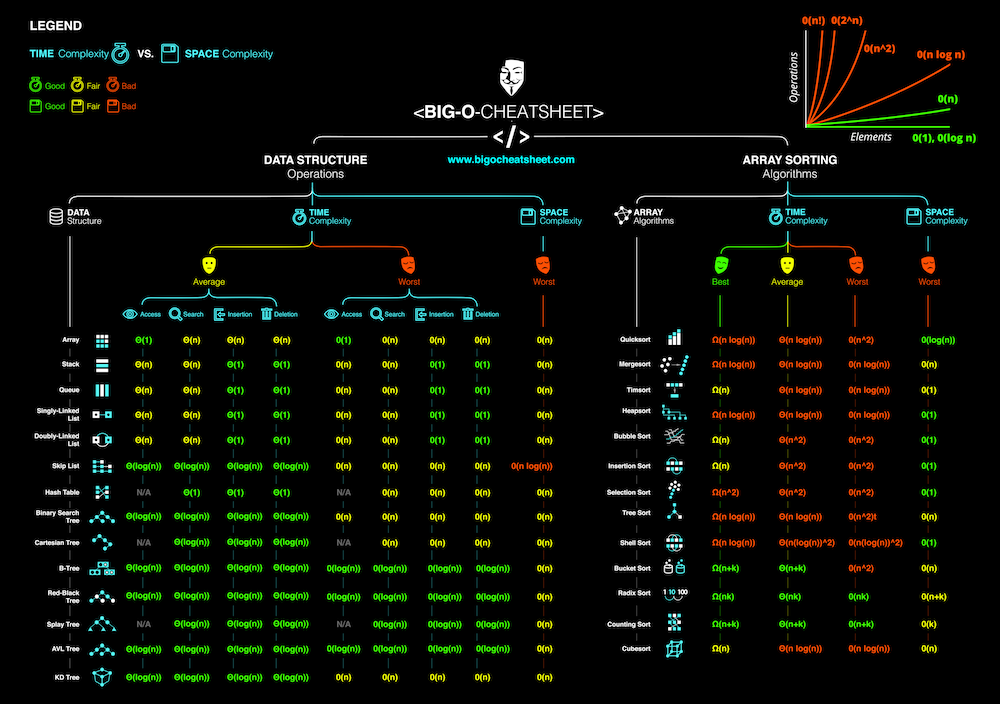
Big-O
- Big-O notation is a notation used to describe how efficient algorithms are.
- Some types of Big-O include:
- O(1)
- O(n)
- O(n\(^2\))
- O(\(\log n\))
- O(2\(^n\))
- O(n!)
The best possible complexity to have in your algorithm is O(1) and the worst complexity is O(n!)
python
for i in range(1, n):
sum++
The bigger the number you put in as n, the longer time the algorithm will take, however this increase is linear and only increases at the same rate as the rate of the increase of n.
python
for i in range(1, n):
for j in range (1, n):
sum++
When you increase n, you increase the time complexity of the algorithm to the power of 2. This is because when you increase n by 1, you are looping over the entire of the second section of code another time which makes the algorithm much slower.
This type of complexity occurs most frequency when you put a loop inside another loop.
Example written in Rust
rust
fn fibonacci(n:i64) -> i64 {
if n < 2 {
return n;
}
return fibonacci(n-1)+fibonacci(n-2)
}
This algorithm calculates the fibonacci number at a certain index.
The function is recursive, and has a complexity of O(\(2^n\))
A binary search is an algorithm with a complexity of log(n).