Regions in Argand Diagrams
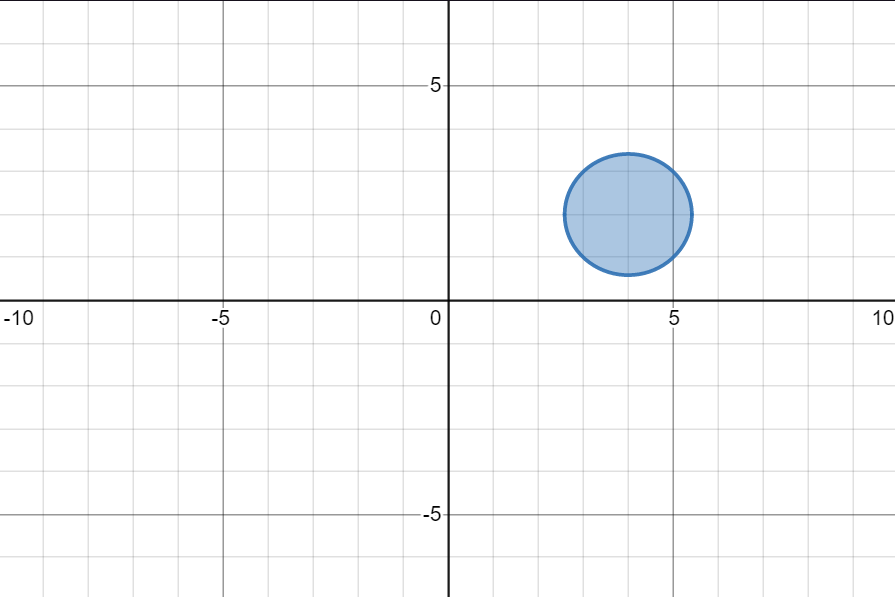
\(|z-4-2i|\leq2\)
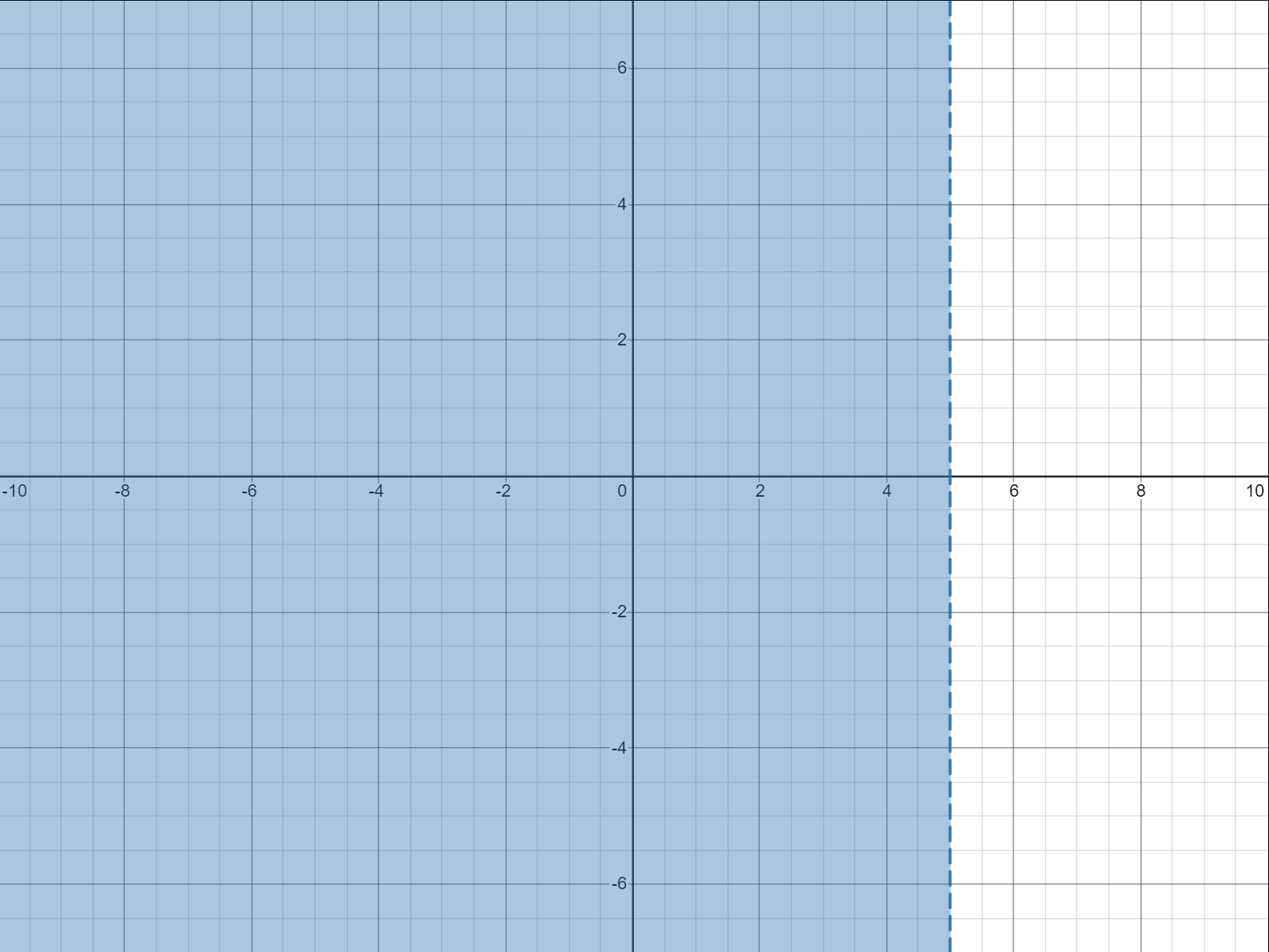
\(|z-4|<|z-6|\)
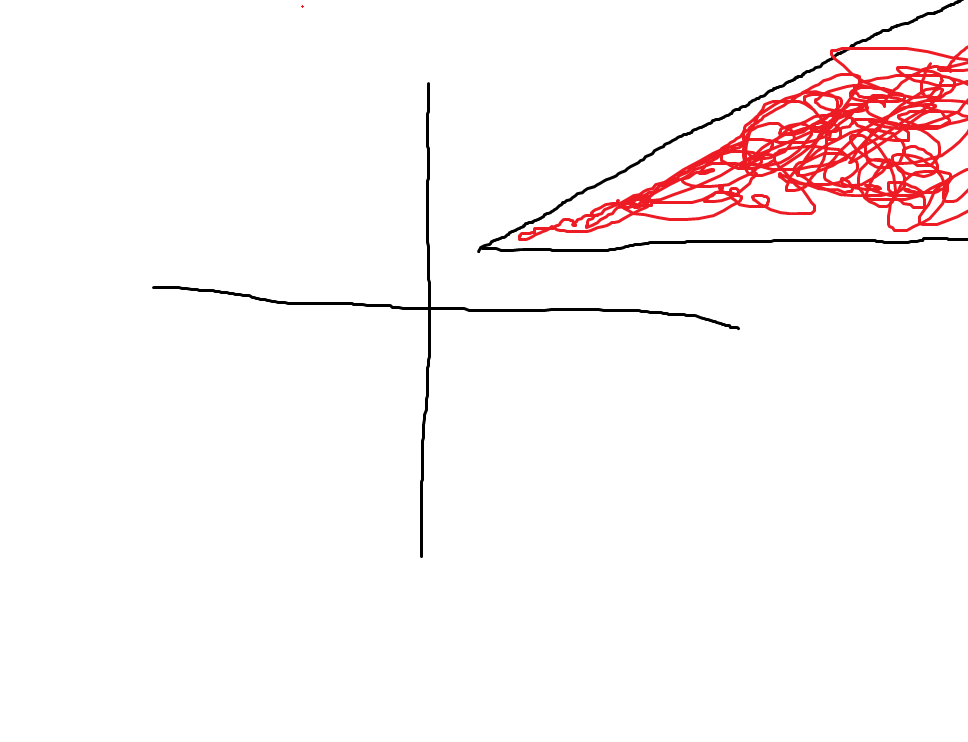
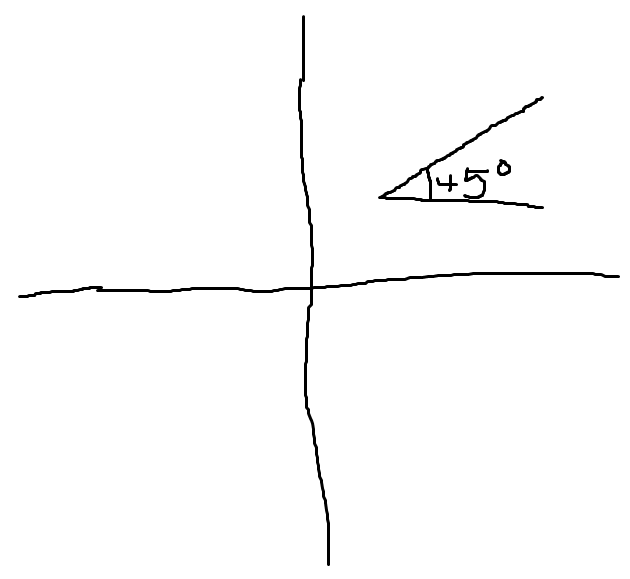
\(0 \leq arg(z-2-2i) \leq \frac{\pi}{4}\)
`
Regions in circlular loci
- For regions in circular loci, if the expression is \(\leq\) to the answer, then the region is inside the circle.
- If the expression is \(\geq\) the answer then the region is outside the circle.
Regions in perpendicular bisector loci
- For regions in perpendicular bisector loci, if one side of the equation is less than the other, then the shaded area is the area on that equation's side of the perpendicular bisector.
- Example: \(|z-3| \leq |z-5|\)
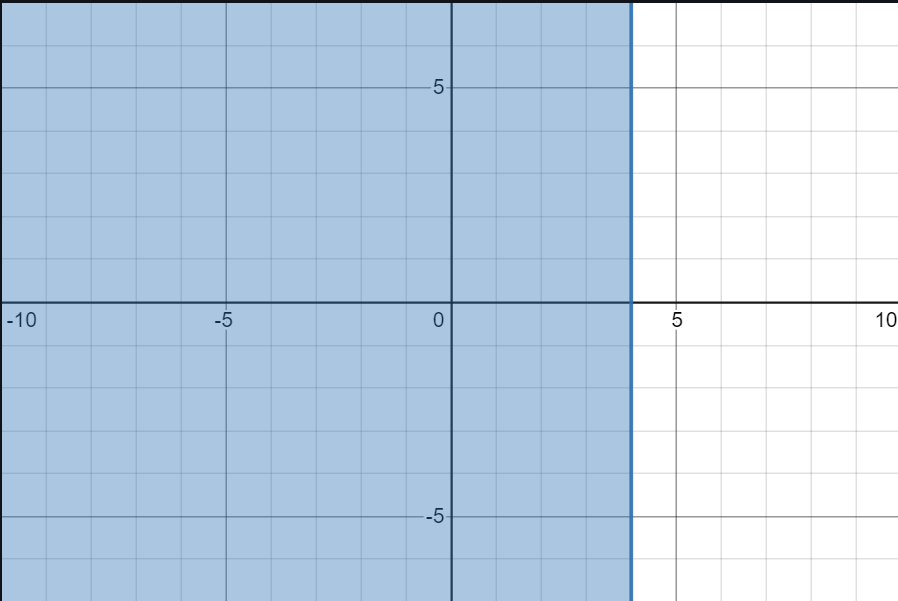
- If we instead flip this, instead we have \(|z-3| \geq |z-5|\)
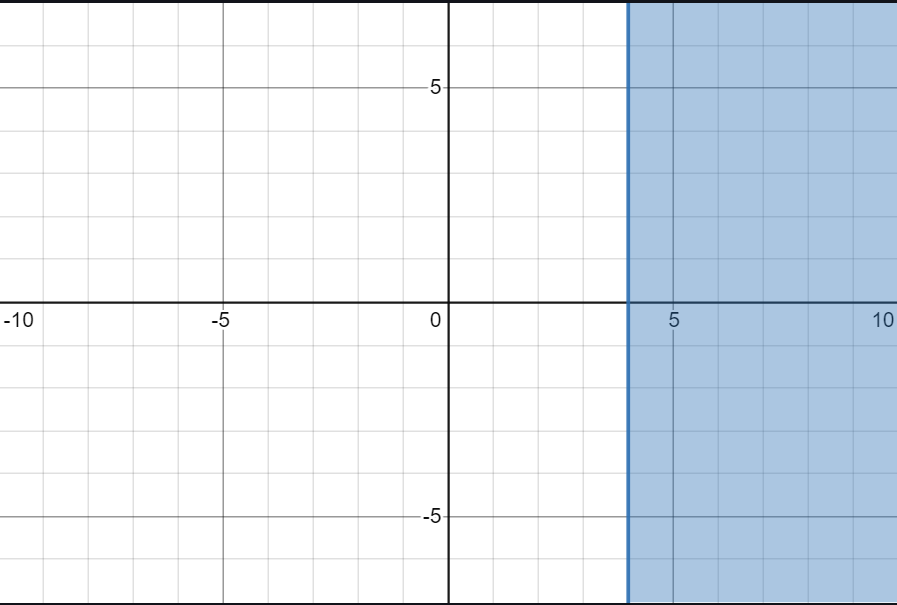
Regions in angle loci (argument form)
- In an angle loci, similarly to the circular loci, if the expression is \(\leq\) the answer, then the region is inside the angle (stretching both ways indefinitely)
- If the expression is \(\geq\) to the answer, then the region is outside the angle.
- Example: \(0\leq arg(z-1-i) \leq \frac{\pi}{4}\)