The Simplex Method
Getting the initial tabloux
- Structure of the table will look like this.

- To fill out the top row, create an equation out of your maximised or minimised expression.
- ** E.G.** \(P = 2x+3y\) becomes \(P-2x-3y=0\)
- This causes our table to become this:
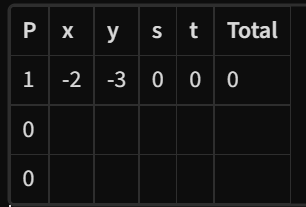
- Next we convert the inequalities to equations by adding slack variables.
- E.G. \(x+2y\leq6\) goes to \(x+2y+s=6\)
- E.G. \(x+y\leq5\) goes to \(x+y+t=5\)
- This makes the table become this:
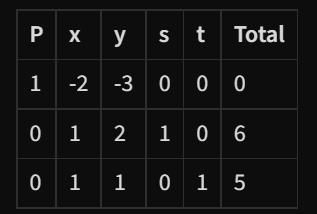
- Our initial table is now formed.
Forming the next tabloux
- To choose the column you want to use, look for your x/y/z variables and find the one which has the largest negitive number.
- For example: on the table we just covered, we would choose the y column because \(-3\) is larger than \(-2\) .
- We now make a new row on the end to store our values we are making now. Divide the total column by the numbers in the y column.
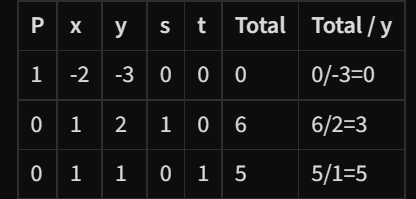
- We now choose the value in the new column with the SMALLEST positive number possible.
- In this example, this would be 3 (0 is not considered positive)
- We now highlight the row and column we selected and draw a ring around our pivot. (the number that is on the selected row and the selected column).

- The pivot we chose is not equal to 1. Therefore we divide the row to make the pivot 1.
- This is our new, divided row.
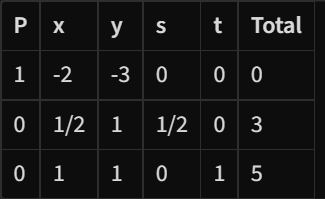
- This ROW is called the pivot row and we will add or subtract this row to the others to make the other rows have 0 in the column we chose.
- Once this is complete and only one box in the column has a 1 in it, we have completed one pass of the simplex method.
BONUS: How to read the Tabloux
- To read the Tabloux, read across the P row at the top. If there is a number that is not 0 in any of the columns, then that value is 0.
- If the number in the P row is 0, then look down the tabloux on that particular column and find the place where a 1 is (usually).
- You then go all the way to the end of that row and look at the value at the end.
- This is your value for the column you started using earlier!