Proving Statements involving Matrices
Prove that \(\begin{pmatrix}1 & -1 \\ 0 & 2\end{pmatrix}^n=\begin{pmatrix}1 & 1-2^n \\ 0 & 2^n\end{pmatrix}\) for all \(n\in \natural\)
- When n=1, LHS = \(\begin{pmatrix}1 & -1 \\ 0 & 2\end{pmatrix}^1=\begin{pmatrix}1 & -1 \\ 0 & 2\end{pmatrix}\)
- Assume holds true for \(n=k\) \(\begin{pmatrix}1 & -1 \\ 0 & 2\end{pmatrix}^k\)
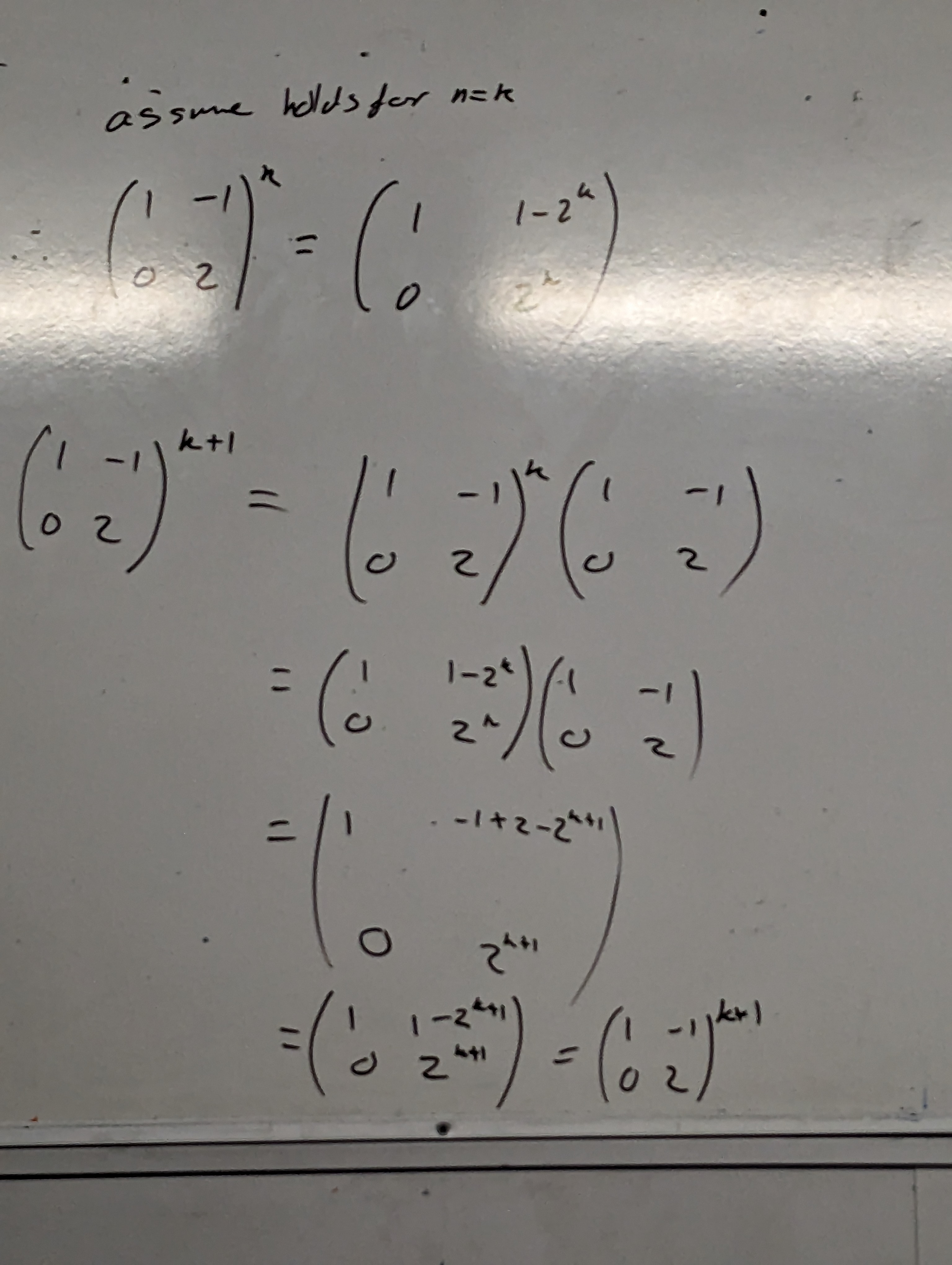
- \(\therefore\) holds true for \(n=k+1\)
- Since true for \(n=1\) and true for \(n=k\), true for \(n=k+1\) and therefore true for all \(n\).