Finding the Derivative
Differentiation from first principles
- Finding the gradient of \(x^2\) at \(x=2\)
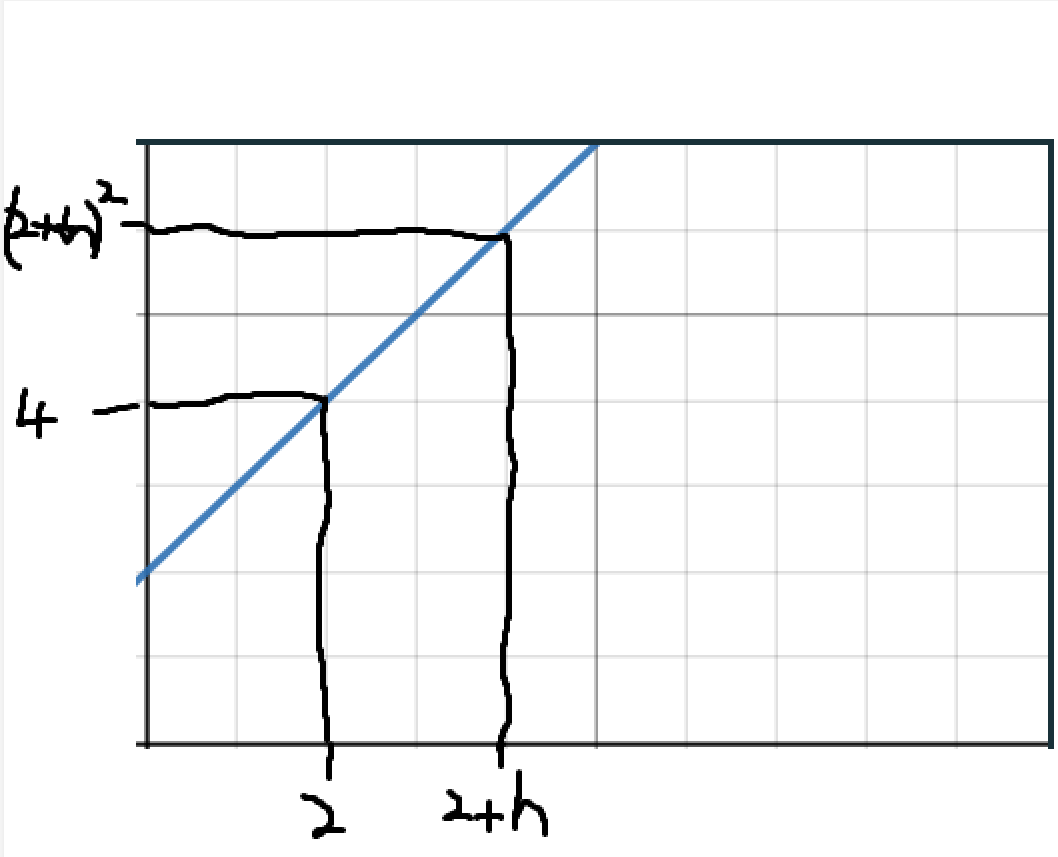
- \(\(m=\lim_{ h \to 0 } \frac{(2+h)^2-4}{h}\)\)
- \(\(m=\lim_{ h \to 0 } \frac{4+h+h^2-4}{h}\)\)
- \(\(m=\lim_{ h \to 0 }\frac{4h+h^2}{h}\)\)
- \(\(m=\lim_{ h \to 0 }4+h\)\)
- \(\(m=4\)\)
Therefore the gradient at \(x=2\) on a \(x^2\) graph is 4.
Finding the derivative
Using the same info from the graph above, but for x
- $$f^{'}(x)=\lim_{ h \to 0 } \frac{f(x+h)-f(x)}{h} $$
- \(\(f^{'}(x)=\lim_{ h \to 0 } \frac{(x+h)^2-x^2}{h}\)\)
- \(\(f^{'}(x)=\lim_{ h \to 0 } \frac{x^2+2xh+h^2-x^2}{h}\)\)
- \(\(f^{'}(x)=\lim_{ h \to 0 } 2x+h\)\)
- \(\(f^{'}(x)=2x\)\)
To find an arbitary \(?x^?\) you multiply the co-efficient of \(x\) by the power.
For \(x^3\) graphs
-
\[f(x)=x^3\]
-
\[f^{'}(x)=\lim_{ h \to 0 } \frac{(x+h)^3-x^3}{h}\]
-
\[f^{'}(x)=\lim_{ h \to 0 } \frac{x^3+3hx^2+3xh^2+h^2-x^3}{h}\]
-
\[f^{'}(x)=\lim_{ h \to 0 } (x^3+3x^2+3xh+h-x^3)\]
-
\[f^{'}(x)=\lim_{ h \to 0 } (3x^2+3xh+h)\]
-
\[f^{'}(x)=3x^2\]
The cheaty method
- Decrement the power by 1, times the original power by the coefficient of \(x^n\) term.
Some questions
- \(y=x^7\), gradient = \(7x^6\)
- \(y=3x^{10}\) gradient = \(30x^9\)
- \(f(x)=\frac{x^{1/2}}{x^2}=x^-{3/2}\to-\frac{3}{2}x^{-\frac{5}{2}}\)
- \(y=ax^{a}\), gradient = \(a^2x^{a-1}\)
- \(f(x)=\sqrt{ 49x^{7 }}\to f(x)^2=49x^7\to f^{'}(x)^2=343x^6\)
More Questions
- \(y=2x^2-3x\to 4x-3\)
- \(y=4-9x^3 \to -27x^2\)
- \(y=5x+1 \to 5\)
- \(y=ax \to a\)
- \(y=6x-3+px^2 \to 6+2px\)
Harder Example
- \(x^2-4x+2 \to 2x-4\)
- -2 is the gradient at (1, -1)
- \(2x-4=5 \therefore x=4.5\)
- \(\frac{17}{4}\) is the y-coordinate