Calculating Angles between Lines and Planes
Linking \(\mathbf{a}, \mathbf{r}\) and \(\mathbf{n}\)
- \(\mathbf{a}\) is the position vector of a fixed point on the plane.
- \(\mathbf{r}\) is the position vector of some non-fixed point on the plane.
- \(\Pi\) is the plane.
- \(\mathbf{n}\) is the normal, which is a vector that is perpendicular to the plane.
- Since \(\mathbf{r}-\mathbf{a}\) is perpendicular to \(\mathbf{n}\), \((\mathbf{r}-\mathbf{a})\times \mathbf{n}=0\)
- This can be rearranged to give, \(\mathbf{r}\times \mathbf{n}=\mathbf{a}\times \mathbf{n}\)
- But since \(\mathbf{a}\times \mathbf{n}\) is a constant, we can replace this with a constant scalar \(\mathbf{p}\)
- \(\therefore\) the equation of a plane = \(\mathbf{r}\times \mathbf{n}=\mathbf{p}\) where \(\mathbf{r}\) is a position vector of some point on the plane, \(\mathbf{n}\) is normal to the plane, and \(\mathbf{p}\) is a scalar constant.
Find the acute angle between the line \(l\) with equation \(\mathbf{r}=2\mathbf{i}+\mathbf{j}-5\mathbf{k}+\lambda(3\mathbf{i}+4\mathbf{j}-12\mathbf{k})\) and the plane with equation \(\mathbf{r}\times(2\mathbf{i}-2\mathbf{j}-\mathbf{k})=2\).
- \(\mathbf{n}=\begin{pmatrix}2 \\ -2 \\ -1\end{pmatrix}\)
- \(\mathbf{b}=\begin{pmatrix}3 \\ 4 \\ -12\end{pmatrix}\)
- \(\mathbf{n}\times \mathbf{b}=10\), \(|\mathbf{b}|=13\), \(|\mathbf{n|=3}\)
- \(\cos^{-1}\left( \frac{10}{13\times3} \right)=75.1\)
- \(\theta=90-75.1=14.9\)
Rule to find the angle between line \(\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}\) and a plane \(\mathbf{r}\times \mathbf{n}=k\)
\[\cos\alpha=\frac{\mathbf{b}\times \mathbf{n}}{|\mathbf{b}||\mathbf{n}|}$$
$$\theta=90-\alpha\]
Angle between two planes
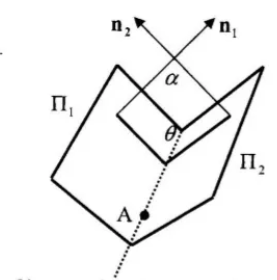
- If we find the two normals of the planes and work out the angle between those, then \(180-\alpha=\theta\)
Exercise 9D Q1b
- \(\mathbf{r}=(\mathbf{i}-\mathbf{j}+7\mathbf{k})+\lambda(-2\mathbf{i}-\mathbf{j}+3\mathbf{k})\)
- \(\mathbf{r}=(8\mathbf{i}+5\mathbf{j}-\mathbf{k})+\mu(-4\mathbf{i}-2\mathbf{j}+\mathbf{k})\)
- Find scalar product:
- \(\begin{pmatrix}-2 \\ -1 \\ 3\end{pmatrix}\times \begin{pmatrix}-4 \\ -2 \\ 1\end{pmatrix}=8+2+3=13\)
- \(\frac{13}{\sqrt{ 14 }\times \sqrt{ 21 }}\)
- \(\frac{13}{7\sqrt{ 6 }}\)
- \(=0.7581\)
- \(\cos \theta=0.7581\)
- \(\theta=40.7^\circ\)
Exercise 9D Q1c
- \(\mathbf{r}=(3\mathbf{i}+5\mathbf{j}-\mathbf{k})+\lambda(\mathbf{i}+\mathbf{j}+\mathbf{k})\)
- \(\mathbf{r}=(-\mathbf{i}+11\mathbf{j}+5\mathbf{k})+\mu(2\mathbf{i}-7\mathbf{j}+3\mathbf{k})\)
- Find scalar product:
- \(\begin{pmatrix}1 \\ 1 \\ 1\end{pmatrix}\times \begin{pmatrix}2 \\ -7 \\ 3\end{pmatrix}=2-7+3=-2\)
- \(\frac{-2}{\sqrt{ 3 }\times \sqrt{ 62 }}\)
- \(\frac{-2}{\sqrt{ 186 }}\)
- \(=0.1466\)
- \(\cos \theta=0.1466\)
- \(\theta=81.57^\circ\)
Find the acute angle between the line \(l\) with equation \(\mathbf{r}=2\mathbf{i}+\mathbf{j}-5\mathbf{k}+\lambda(4\mathbf{i}+4\mathbf{j}+7\mathbf{k})\) and the plane with equation \(\mathbf{r}\times(2\mathbf{i}+\mathbf{j}-2\mathbf{k})=13\).
- \(\mathbf{n}=\begin{pmatrix}2 \\ 1 \\ -2\end{pmatrix}\)
- \(\mathbf{b}=\begin{pmatrix}4 \\ 4 \\ 7\end{pmatrix}\)
- \(\mathbf{n}\times \mathbf{b}=-2\), \(|\mathbf{b}|=9\), \(|\mathbf{n|=3}\)
- \(\cos^{-1}\left( \frac{\mid-2\mid}{\underbrace{ 9\times3 }_{ 27 }} \right)=85.75\)
- \(\theta=90-85.75=4.25\)