Two-Stage Simplex Method

• Two stage simplex is used when the origin point is outside the feasible region.
• This is the case when there is an inequality that uses the greater than sign (\(\geq\))

Problem:
- Max \(P=3x-2y+z\)
Bounds:
- \(x+y+2z\leq10\)
- \(2x-3y+z\geq5\)
- \(x+y\geq 8\)
- \(x,y,z\geq 0\)

Solve:
- \(x+y+2z+s=10\)
- \(2x-3y+z-t+a_{1} = 5\)
- \(x+y-u+a_{2}=8\)
From these new equations we generate a new function called \(\mathbf{I}\).
At the end of this simplex pass, \(\mathbf{I}\) has to be equal to 0. If this function doesnt equal 0, we can just stop halfway through because there will be no solution to the problem.
- \(\mathbf{I}=-(a_{1}+a_{2})\)
- We rearrange to get \(a_{1}\) and \(a_{2}\) in terms of the other variables and numbers.
- \(I=-(5-2x+3y-z+t+8-x-y+u)\)
- \(I = -13+3x-2y+2-t-u\)
- \(I-3x+2y-z+t+u=-13\)

- We then write out a tabloux and have a new row for the I values.

- We then perform simplex on the I row, using the exact same method we used for our P row in one stage simplex.
- Once there are no more negative values in your \(\mathbf{I}\) row, if there is a value in your I row for the total that is not 0, there are no solutions.
- If there is a 0 when you finish, there is a feasible solution.


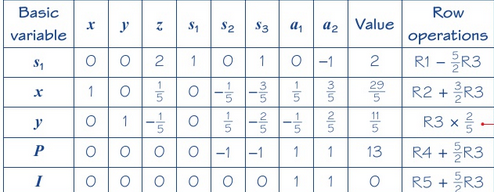
- If this happens, you now remove the \(a_{1}\) , \(a_{2}\) and \(\mathbf{I}\) variables and their respective columns and then perform normal simplex on the remaining tabloux.

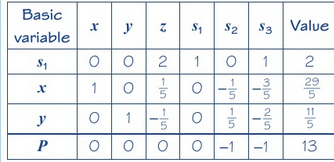
- Done!

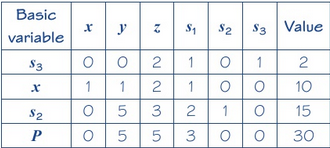
(Note: This simplex version is very long in comparison to the Big M method)