Conservation of Momentum

Conservation

\[m_{1}u_{1}+m_{2}u_{2}=m_{1}v_{1}+m_{2}v_{2}\]

Example

Before Collision
- Ball 1: \(2kg\), \(4ms^{-1}\)
- Ball 2: \(1kg\), \(0ms^{-1}\)

After Collision:
- Ball 1: \(2kg\), \(2ms^{-1}\)
- Ball 2: \(1kg\), \(?ms^{-1}\)

\(2(4)+1(0)=2(2)+1(v)\)
\(8=4+v\)
\(v=4ms^{-1}\)

Exercise 1B Q1

A particle P of mass \(2kg\) is moving on a smooth horizontal plane with speed \(4ms^{-1}\). It collides with a second particle Q of mass \(1kg\) which is at rest. After the collision P has speed \(2ms^{-1}\) and it continues to move in the same direction. Find the speed of Q after the collision.

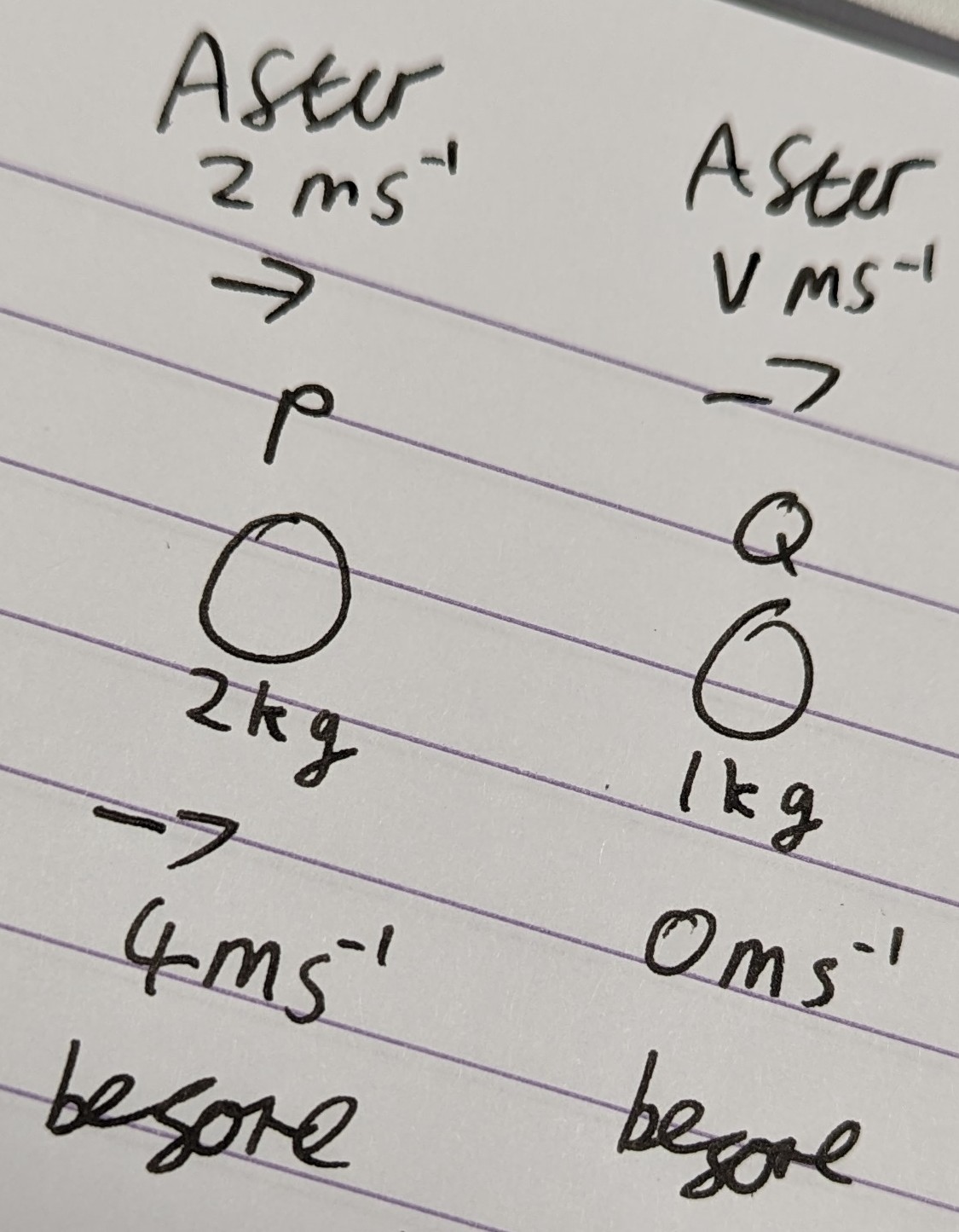
- \(4(2)=2(2)+1(v)\)
- \(v=4\)

Exercise 1B Q2

A railway truck of mass 25 tonnes moving at \(4ms^{-1}\) collides with a stationary truck of mass 20 tonnes. As a result of the collision the trucks couple together.
Find the common speed of the trucks after the collision.

\(25(4)=45(v)\)
\(v=\frac{100}{45}=2\frac{2}{9}ms^{-1}\)

Exercise 1B Q3

Particles A and B have masses \(0.5 kg\) and \(0.2 kg\) respectively. They are moving with speeds \(5ms^{-1}\) and \(2ms^{-1}\) respectively in the same direction along the same straight line on a smooth horizontal surface when they collide. After the collision A continues to move in the same direction with speed \(4ms^{-1}\). Find the speed of B after the collision.

- \(0.5(5)+0.2(2)=0.5(4)+0.2(v)\)
- \(2.5+0.4=2+0.2v\)
- \(0.9=0.2v\)
- \(v=4.5\)

Conservation of Momentum

Backlinks