Functions and Mappings
Mappings
- A mapping is a function if every input has a distinct output. Functions can either be one to one or many to one.
- One to many is not a function.
- You can convert a mapping into a function by restricting the domain.
Domain and range.
- The domain is the number you start with and the range is the number/numbers you end with.
- AKA: The domain is where a function starts, and the range is where the function finishes.
Examples of [Functions(/a-level/maths/pure-1/quadratics/functions.html)
- \(x+1\) is a one to one function. (e.g. \(5\to6\))
- \(x^2\) is a many to one function. (e.g. \(2\to4\) and \(-2\to4\))
- \(\sqrt{ x }\) is a one to many function. (e.g. \(4\to -2\text{ or }2\))
Graph of \(y=\sqrt{ x }\)
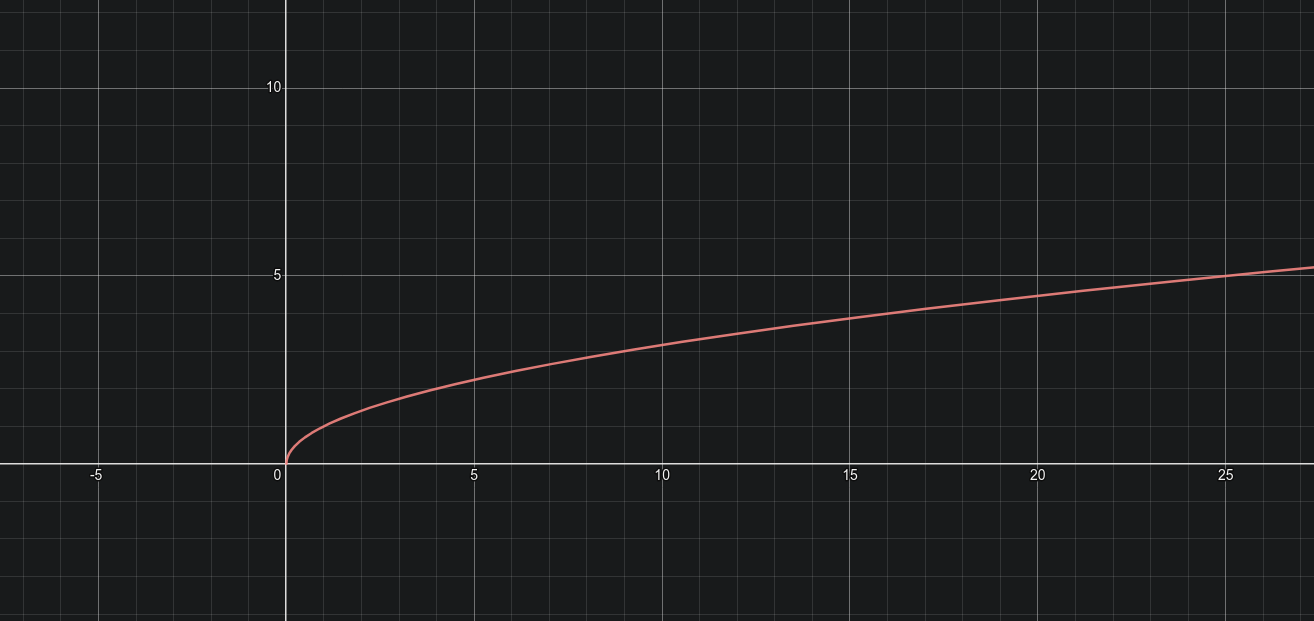
- You cannot square root a negative number therefore we restrict the domain to \(x\geq0\). This is because if we apply this function to values less than 0, we dont get a value at all.
Set Notation
- Always use curly brackets: {}
- Inside these brackets, we put a range of values for which \(x\) is applicable.
- E.G. \(x \in \mathbb{Z}\) (integer), \(x \in \mathbb{R}\) (rational)
- To seperate statements inside set notation we use commas (,)