Faraday's Law and Lenz's Law

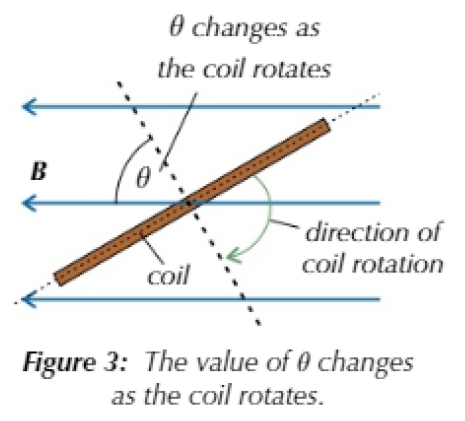
• When a coil such as that in Figure 3 rotates uniformly (at a steady speed) in a magnetic field, the coil cuts the flux and an alternating e.m.f. is induced.
  
• The amount of flux cut by the coil (flux linkage) is given by:
• \(N\phi = BAN\cos\theta\).

• As the coil rotates, \(\theta\) changes so the flux linkage varies sinusoidally between \(+BAN\) and \(-BAN\).
• How fast \(\theta\) changes depends on the angular speed \(\omega\) of the coil \(\theta=\omega t\)
• \(N\phi=BAN\cos\omega t\)

• The induced emf depends on the rate of change of flux linkage (Faraday's Law) so it also varies sinusoidally.
• The equation for emf at time=\(t\) is: \(\varepsilon=BAN\omega \sin\omega t\)

The shape of the graph of induced e.m.f. can be altered by changing the speed of rotation or the size of the magnetic field:
- Increasing the speed of rotation will increase the frequency and increase the maximum e.m.f.
- Increasing the magnetic flux density \(B\) will increase the maximum e.m.f., but will have no effect on the frequency.

• AC electricity alternates sinusoidally with a frequency of 50hz and a peak potential difference of 325 volts.
• An oscilloscope trace can be used to analyse a wave and measure the time period and peak potential difference.
• The root mean squared of both current and potential difference can be used to calculate the power rating of an AC supply.