Loci in Argand Diagrams
Loci satisfy a set of restrictions
E.G. |z| = 3
This would form a circle of radius 3 at the origin
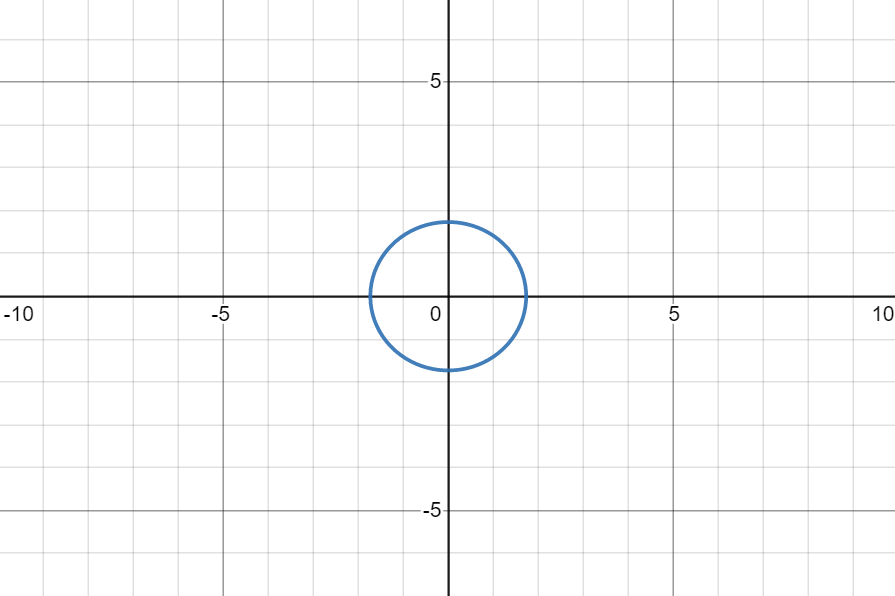
In the form |z-z1 = r|
The difference between some point z from a fixed point z1 is of length r.
i.e. the point z is distence r from point z1
|z-z1 = r| is represented by a circle centre (x1,y1) with radius r, where z1 = x1+iy1
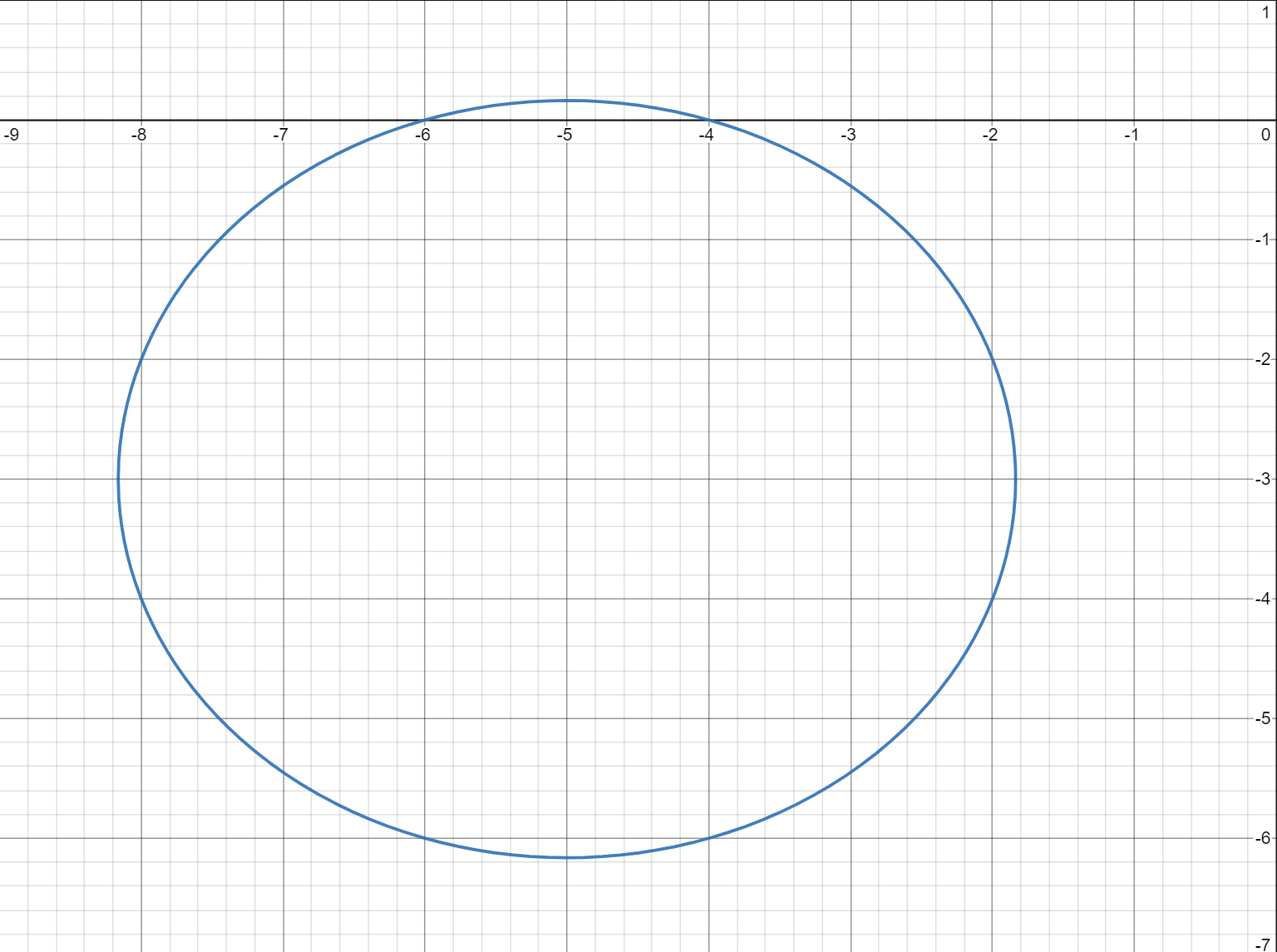
If \(z = x+iy\), then \(z-5-3i = 5\)
\(\therefore x+iy-5-3i = 5\)
\(\therefore (x-5)+i(y-3) = 5\)
This gives the centre of the circle that can be used to define the loci.
In the form |z-z1| = |z-z2|
- The distance of z from z1 is the same as the distance from z2.
- So to solve this, you need to find the point \(z\) that satisfies this.
- The locus of the points that satisfy this will be in the form of a perpendicular bisector.
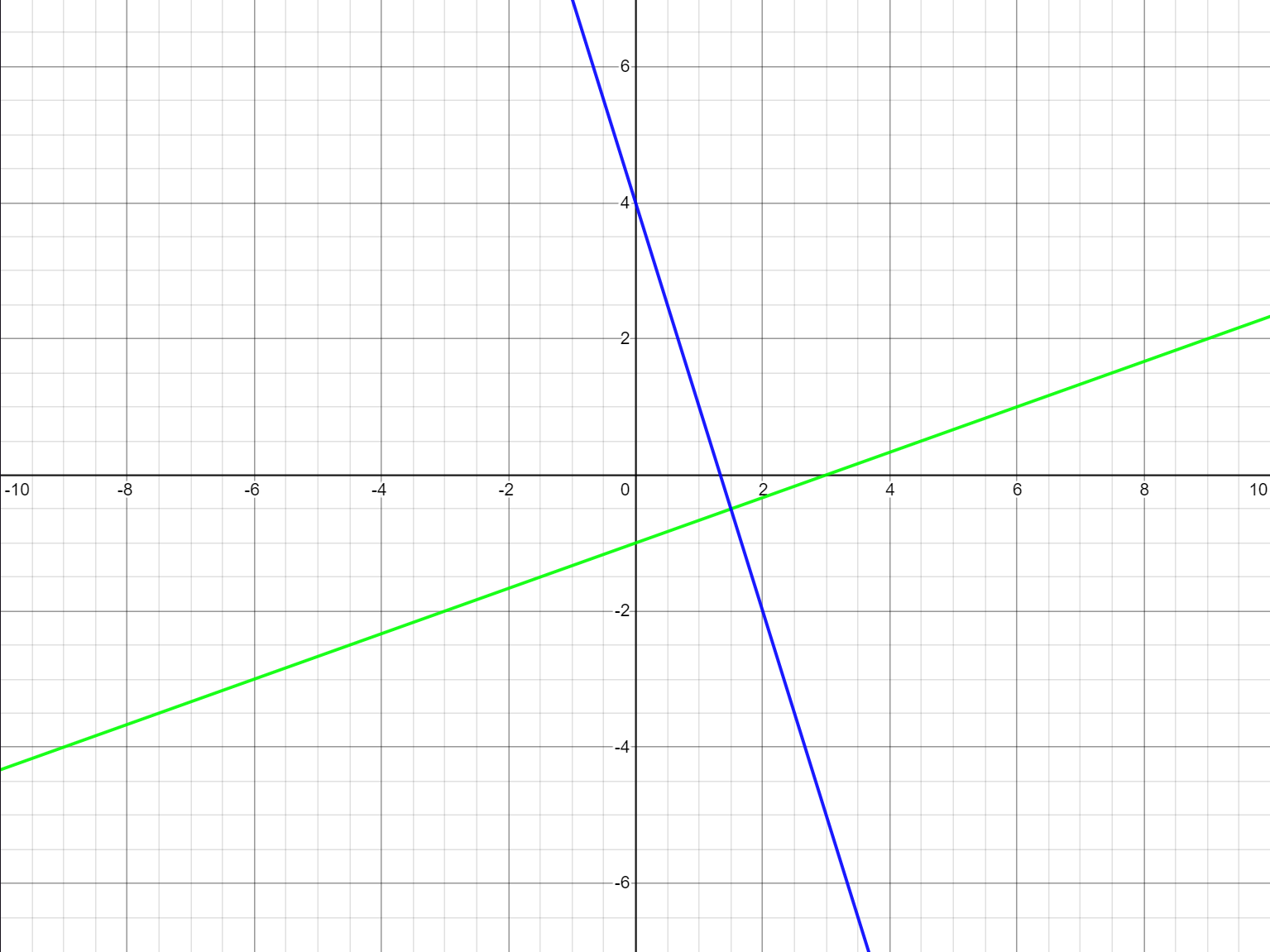
\(|z-3| = |z+i|\)
\(|x+iy-3 = |x+iy+i|\)
\(|(x-3)+iy| = |x+(y+1)i|\)
\(\sqrt{(x-3)^{2} + iy} = \sqrt{ x^2 +(y+1)^2}\)
\((x-3)^{2}+y^{2}= x^{2}+ (y+1)^2\)
Cancelling: \(-6x+9 = 2y+1\)
\(2y = -6x+8\)
\(y = -3x+4\)
Finding minimum and maximum points for a circle
The mimimum and maximum of a locus is the closest and furtherest away point from the origin of the locus.
To find the mimimum and maximum of a locus, you need to first find the distance from the origin to the midpoint:
- Use Pythag to find the distance to the midpoint from the origin.
- Then, subtract or add the radius to find the minimum and maximum points respectively.
\(|z-12-5i| = 3\)
- Find the mid point: (12, 5)
- Find the distance to the midpoint from the origin (13)
- Minimum = distance - radius (\(13-3=10\))
- Maximum = distance + radius (\(13+3 = 16\))
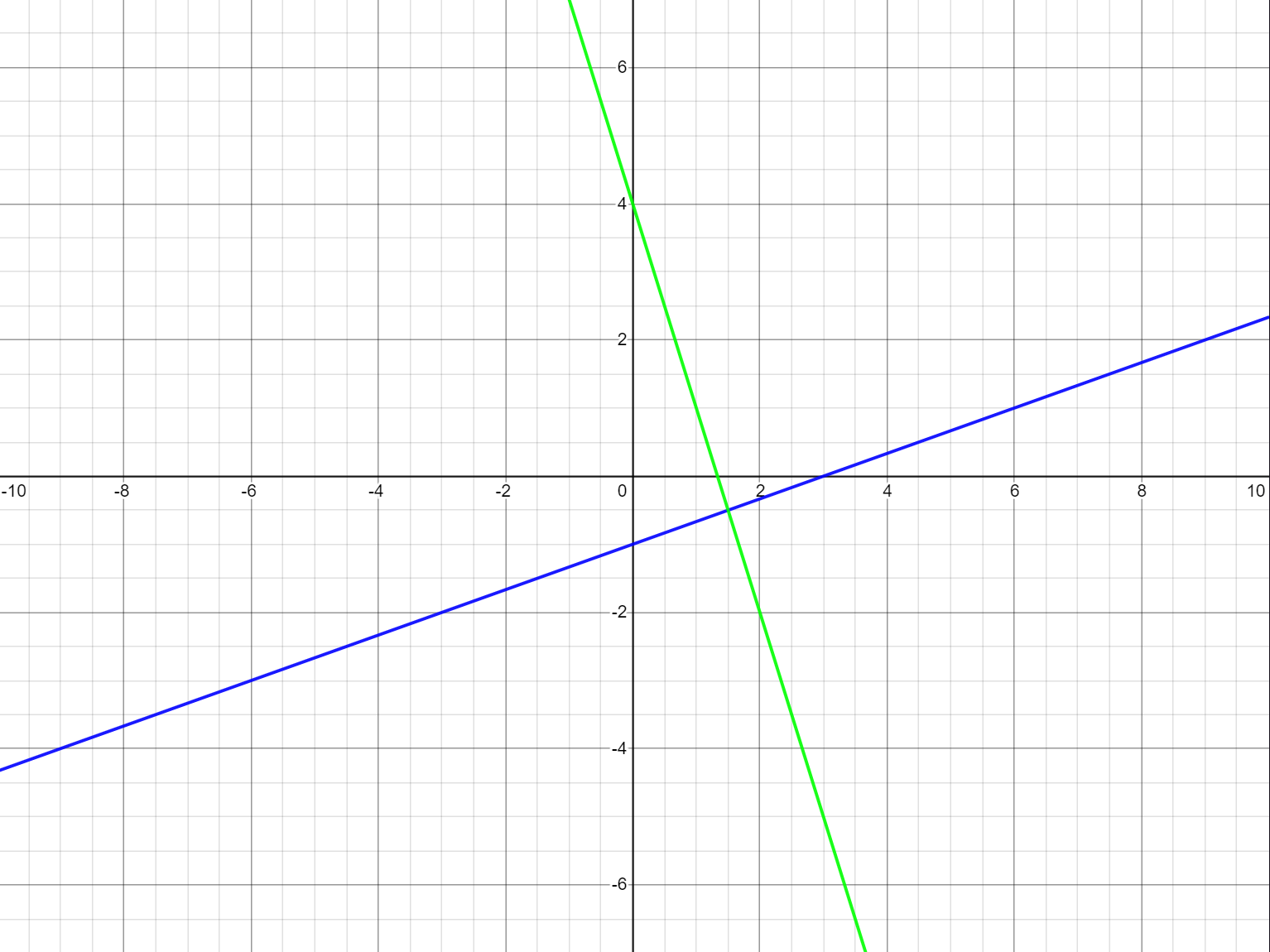
Finding the minimum for a perpendicular bisector
- First calculate the gradient of the perpendicular bisector.
- \(\therefore\) the gradient of the line perpendicular to the perpendicular bisector = the negetive reciprocal
- Substitute back into the original to make a simultaneous equation
- Solve the simultaneous equation for x
- Sub x in and solve for y
- Gradient of perependicular = -3
- Gradient of perpendicular of perpendicular = 1/3
- \(y = \frac{1}{3}x\)
- \(\frac{1}{3}x = -3x+4\)
- \(\frac{10}{3}=4\)
- \(x=\frac{12}{10} = \frac{6}{5}\)
- \(\therefore y=\frac{4}{10}=\frac{2}{5}\)
- Minimum = \(\frac{6}{5}, \frac{2}{5}\)
Rewrite it:
- \(|z-5|=|z-(2+3i)|\)
- \(| x+iy-5| = | x+iy-(2+3i)|\)
- \(|(x-5)+iy| = |(x-3)+(y-3)i|\)
- \(\sqrt{ (x-5)^{2}+y^{2}} = \sqrt{ (x-2)^2 +(y-3)^2}\)
Expand it:
- \(x^2-10x+25+y^2=x^2-4x+y^2-6y+13\)
Cancel:
- \(-10x+25=-4x-6y+13\)
- \(6y=6x-12\)
- \(y=x-2\)
Perpendicular gradient = -1
Simultaneous Equations:
- \(y=-x\)
- \(-x=x-2\)
- \(2x=2\)
- \(x=1\)
\(y=-1\times 1=-1\)
Point = 1, -1
\(\sqrt{ 1^{2}+(-1)^{2 }}=\sqrt{ 2 }\)
\(|z|\) minimum \(= \sqrt{ 2 }\)
In the form arg(z-z1) = \(\theta\)
At any point, the angle made relative to the origin is \(\frac{\pi}{6}\)
- \(arg(z) = \frac{\pi}{6}\)
- \(arg(x+iy) = \frac{\pi}{6}\)
- \(\frac{y}{x} = \tan\left( \frac{\pi}{6} \right) = \frac{1}{\sqrt{ 3 }}\)
- \(y = \frac{1}{\sqrt{ 3 }}x\)
- \(z+3+2i\) can be written as \(z-(-3-2i)\)
One way of thinking about it: - If we were to add \(3+2i\) to \(z-(-3-2i)\), then we would have \(arg(z) = \frac{3\pi}{4}\) wich would be centred at the origin.
- ???
- \(y+2=-1(x+3)\)
- \(y+2=-x-3\)
- \(y = -x-5\)
\(x < -3\)
\(y > -2\)
This is because the line stops at the point (-3,-2)